В правильном тетраэдре все грани - равные равносторонние треугольники.
Площадь одной грани:
S₁ = a²√3/4 = 4²√3/4 = 4√3 см²
Так как К - середина DC, то АК = ВК - медианы и высоты равных треугольников DAC и DBC. Тогда
Sakd = Sbkd = 1/2 S₁ = 2√3 см² - это площади двух боковых граней пирамиды KABD.
Пусть Н - середина АВ, так как треугольник АКВ равнобедренный, то КН - его высота.
СН = DH = а√3/2 = 4√3/2 = 2√3 см как медианы и высоты равных равносторонних треугольников.
Тогда ΔDHC равнобедренный, КН - его медиана и высота:
КН⊥CD.
ΔСКН: ∠СКН = 90°, СН = 2√3 см, СК = CD/2 = 2 см, по теореме Пифагора
КН = √(CH² - CK²) = √((2√3)² - 2²) = √(12 - 4) = √8 = 2√2 см
Sabk = 1/2 AB · KH = 1/2 · 4 · 2√2 = 4√2 см²
Площадь боковой поверхности пирамиды KABD:
Sбок = Sakd + Sbkd + Sabk = 2√3 + 2√3 + 4√2 = 4(√3 + √2) см²
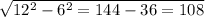
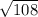
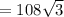
Sбок= Р*h Sбок=(АВ+ВС+СД ) * АА1
1) т.к угАСВ=90* по условию, и призма прямая, то двугранный угол АСС1В1 =90* . значт угА1СВ=90*
2) рассмотрим треуг А1СВ=прямоуг, угС=90*, СА1В=30*, А1В=10см,
СВ=А1В * sin30* CB=5cm
3) рассмотрим АВС-прямоуг, угС=90* АС=СВ=5см, т.е АВС равнобедренный
по тПифагора АВ= sqrt 2AC^2 AB=5sqrt2
4) рассмотрим АА1В- прямоугольный , угА=90, АВ=5sqrt2 , А1В=10
из тПифагора АА1=sqrt ( A1B^2 -AB^2) AA1=sqrt(100- 50)= 5sqrt2
5) Sбок = (5sqrt2 + 5 + 5 ) * 5 sqrt2 =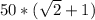 cm
cm