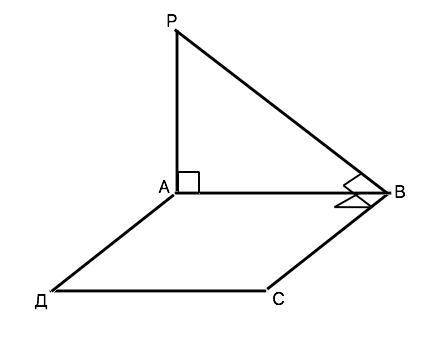
РА - перпендикуляр к площади параллелограмма АВСД. Укажите вид параллелограмма, если РВ перпендикулярен ВС. а) ромб, б) прямоугольник; в) квадрат.
Объяснение: РВ - наклонная. АВ - её проекция на плоскость АВСД. По т. о 3-х перпендикулярах если наклонная (РВ) перпендикулярна прямой (ВС) на плоскости, то её проекция на ту же плоскость перпендикулярна данной прямой. Следовательно, АВ⊥ВС, и угол АВС - прямой. Противоположные углы параллелограмма равны. ⇒ ∠Д=∠В=90°, поэтому из суммы углов четырехугольника ∠А+∠С=360°-2•90°=180°, и каждый из них равен 180°:2=90°.
Углы четырехугольника АВСД прямые. ⇒ АВСД - прямоугольник. Он может быть и квадратом. если его стороны будут равны.
2) по 2-м сторонам и углу между ними
3) по 3-м сторонам
4) по 2-м сторонам и углу между ними
5) по 2-м сторонам и углу между ними
Объяснение:
2) углы ROS и TOP равны (вертикальные)=> треугольники равны по RO=OT, SO=OP (по условию) и вертикальным углам.
3) треугольники ABD и ACD:
AB=AC, BD= CD( по условию), а AD - общая сторона=> треугольники равны по сторонам.
4) из треугольников ABC и MKE:
BO=OP=PC=KD=DF=FE=> BC=KE
углы C и E равны по условию, так же как и стороны AC и ME => треугольники равны по сторонам и углу между ними.
5) AE- общая, AEB=AEC( их внешние углы равны) => треугольники равны по 2-м сторонам и углу между ними.
По правилу нахождения разности векторов:
АК-АВ=ВК. Или
ВК=(1/3)*b - a.
P.S. Правило: Для получения вектора разности (c) = (a-b) начала векторов соединяются и началом вектора разности (c) будет конец вектора (b) (вычитаемое), а концом — конец вектора (a) (уменьшаемое).