В прямоугольном треугольнике a
и
b
- катеты,
c
- гипотенуза.
Найдите
a
, если
b
=
0
,
4
и
c
=
0
,
5

👇

Увидеть ответ

Ответ:

matvee1

22.07.2020

ответ:/2- вторая Степень

А/2+ В/2= С/2

0,5/2=0,25

0,4/2=0,16

0,25-0,16=0,09

С=0,3

Объяснение:

4,4(52 оценок)

Открыть все ответы

Ответ:

ЛераТян2000

22.07.2020

Дана правильная шестиугольная пирамида SABCDEF, в основании которой лежит правильный шестиугольник. Если стороны основания AB=BC=CD=DE=EF=18, то AO=BO=CO=DO=EO=FO=18. И тогда в прямоугольном треугольнике, например ΔSOD, образованном высотой SO, боковым ребром SD=15 и проекцией бокового ребра на основание DO, катет DO=18 будет больше гипотенузы SD=15. То есть, боковые ребра у пирамиды с такими размерами не сойдутся сверху в вершину S.

В условии задачи ОШИБКА! Такая пирамида не существует.

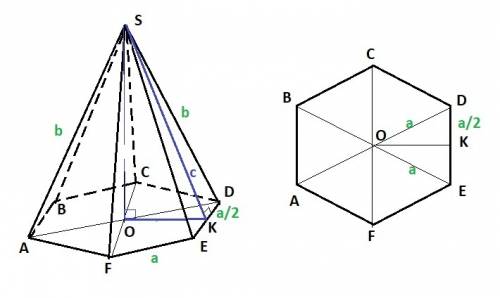
Тогда рассмотрим решение этой задачи в общем случае. Пусть боковые ребра SA=SB=SC=SD=SE=SF=b, стороны основания AB=BC=CD=DE=EF=AF=a.

Площадь боковой поверхности пирамиды состоит из шести равных равнобедренных треугольников.

ΔESD - равнобедренный, SE=SD=b, ED=a. Высота равнобедренного треугольника SK также является медианой ⇒ EK=KD=a/2

ΔSKD - прямоугольный, ∠SKD=90°. По теореме Пифагора

SD² = SK² + KD² ⇒ SK² = SD² - KD² = b² - (a/2)²

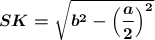
$\boldsymbol{SK=\sqrt{b^2-\Big(\dfrac{a}{2}\Big)^2}}$

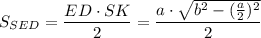
$S_{SED}=\dfrac{ED\cdot SK}{2}=\dfrac{a\cdot \sqrt{b^2-(\frac{a}{2})^2}}{2}$

Площадь боковой поверхности пирамиды

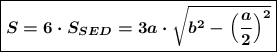
$\boxed {\boldsymbol {S = 6\cdot S_{SED}=3a\cdot \sqrt{b^2-\Big(\dfrac{a}{2}\Big)^2}}}$

===========================================

Допустим, боковое ребро пирамиды b=13, сторона основания a=10

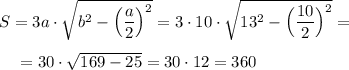
$S = 3a\cdot \sqrt{b^2-\Big(\dfrac{a}{2}\Big)^2}} = 3\cdot 10\cdot \sqrt{13^2-\Big(\dfrac{10}{2}\Big)^2} =\\ \\ ~~~~=30\cdot \sqrt{169-25} =30\cdot 12=360$

==============================================

Допустим, боковое ребро пирамиды b=41, сторона основания a=18

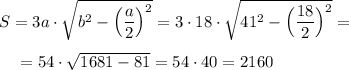
$S = 3a\cdot \sqrt{b^2-\Big(\dfrac{a}{2}\Big)^2}} = 3\cdot 18\cdot \sqrt{41^2-\Big(\dfrac{18}{2}\Big)^2} =\\ \\ ~~~~=54\cdot \sqrt{1681-81} =54\cdot 40=2160$

Стороны основания правильной шестиугольной пирамиды равны 18, боковые ребра равны 15. найдите площад

4,7(58 оценок)

Ответ:

vitalicc

22.07.2020

Если действительно надо найти ВЕ, то зная, что АЕ - медиана, которая по определению делит сторону ВС пополам, имеем:ВЕ=ЕС=28,5см. Это ответ.
Но для чего нам даны стороны АВ и АС?

Скорее всего, в задаче требовалось найти медиану АЕ.
Тогда, зная, что медиана делит треугольник на два РАВНОВЕЛИКИХ, мы можем найти медиану АЕ через равенство площадей треугольников АВЕ и АСЕ, которые находим по формуле Герона: S=√[p(p-a)(p-b)(p-c)].
В нашем случае, для треугольника АВЕ полупериметр равен р=(78,2+АЕ)/2.
Для треугольника АСЕ полупериметр равен р=(68,7+АЕ)/2.
Тогда, освободившись от корня, имеем:
Sabe²=((78,2+АЕ)/2)*((78,2-АЕ)/2)*((АЕ-21,2)/2)((АЕ+21,2)/2)=
(78,2²-АЕ²)*(АЕ²-21,2²)/16.
Sace²=((68,7+АЕ)/2)*((68,7-АЕ)/2)*((АЕ-11,7)/2)((АЕ+11,7)/2)=
(68,7²-АЕ²)*(АЕ²-11,7²)/16.
Sabe²=Sace². Пусть АЕ²=х. тогда
(78,2²-х)*(х-21,2²)=(68,7²-х)*(х-11,7²)
Дальше сплошная арифметика:
78,2²х-х²-78,2²*21,2²+21,2²х=68,7²х-х²-68,7²*11,7²+11,7²х.
х(78,2²+21,2²-68,7²-11,7²)=78,2²*21,2²-68,7²*11,7².
х(9,5*146,9+9,5*32,9)=1657,84²-803,79².
1708,1*х=854,05*2461,63. Отсюда х=1230,815.
Тогда АЕ=√1230,815≈35,08
ответ: медиана АЕ≈35,1.

4,5(86 оценок)

Это интересно:

10.01.2022

10 советов, как повзрослеть после совершеннолетия и принять ответственность за свою жизнь...

Кулинария-и-гостеприимство

06.06.2022

Как приготовить конфеты из сахара...

Компьютеры-и-электроника

06.03.2022

Как сбросить пароль учетной записи на Instagram: мастер-класс с шаг за шагом инструкцией...

Компьютеры-и-электроника

11.08.2021