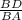2) Рассмотрим треугольник AOC - равнобедренный, т.к. AO=OB: в нём OB_1 является высотой (так как BB_1 - высота), значит, OB_1 - медиана, а значит, AB_1=B_1C Рассмотрим треугольник ABC: BB_1 - высота (по условию задачи) и медиана (так как AB_1=B_1C по доказанному), значит ABC - равнобедренный треугольник, и BB_1 - биссектриса угла В. Пусть расстояние от точки O до AB равно OM; OM = 1 по условию. Пусть расстояние от точки O до BC равно ON. Рассмотрим треугольники MOB и NOB -прямоугольные (<BMO=<BNO=90) OB - общая сторона <MBO=<NBO (т.к. BB_1 - биссектриса) Значит, треугольники MOB и NOB равны по гипотенузе и острому углу, значит OM=ON=1 ответ: 1
На готовом чертеже выразить вектор.
Объяснение:
1)Т.к. AD=СЕ и DB=BE , то AB=BC .
2) ΔBDE подобен ΔBAC по равному углу ( ∠В-общий ) и двум пропорциональным сторонам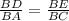
см п.1 . В подобных треугольниках соответственные углы равны ⇒
∠BDA=∠BAC ⇒ DE║AC, секущая АВ ⇒ длина отрезка DE=k*AC.
k=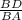
, значит вектор DE= - АС*