
Проводится прямая, параллельная диагонали длины 3 из вершины верхнего (малого) основания, куда приходит диагональ длины 5. Нижнее (большое) основание продолжается до пересечения с этой прямой. Получился треугольник, у которого боковые стороны 3 и 5.
Площадь этого треугольника равна площади трапеции, поскольку у них общая высота и одинаковая средняя линяя.
Легко показать простым вычислением положения концов, что медиана этого треугольника параллельна отрезку, соединяющему середины оснований, а поэтому она ему равна, то есть её длина 2.
Теперь продолжим медиану на её собственную длину 2 за основание (НЕ ЗА ВЕРШИНУ:))) и соединим с вершинами основания ТРЕУГОЛЬНИКА. Получился параллелограмм (поскольку в нем диагонали делятся пополам, этого достаточно). Ясно что его стороны 3 и 5, а одна из диагоналей 4. Рассмотрим, так сказать, "другую половину" этого параллелограма.
Легко видеть что это - прямоугольный треугольник со сторонами 3,4,5.
Его площадь 3*4/2 = 6 равна площади трапеции.
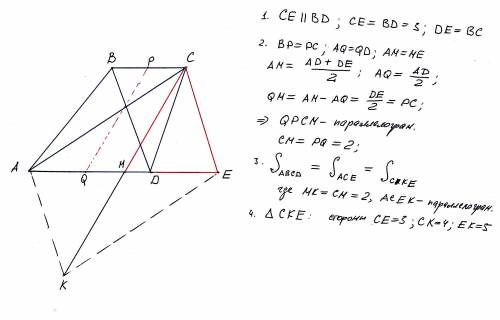
Все пояснения на рисунке
Стороны Δ АВС равны АС=12 м, ВС=16 м и АВ=20 м, СН - высота.
Для данных величин выполняется равенство:
20² = 12² + 16²
400 = 144 + 256
400 = 400
тогда по теореме, обратной теореме Пифагора, данный треугольник - прямоугольный. Большая сторона АВ - гопотенуза = 20, .
Тогда высота СН , проведенная из вершины прямого угла С, опущена на гипотенузу АВ и делит треугольник на два подобных треугольника, каждый из которых подобен Δ АВС.
Рассмотрим подобие треугольников АСН и АВС:
СН/СВ = АС/АВ
СН/16 = 12/20
СН = 16*12/20
СН = 48/5
СН = 9,6
ответ: высота равна 9,6 м.