FG - отрезок средней линии, так как точки пересечения биссектрис F и G - центры окружностей которые касаются одной боковой стороны и двух оснований, то есть они равноудалены от оснований. Через F и G проводим высоты (=диаметры, соединяющие точки касания окружностей с противоположными основаниями). Точки касания обозначим М (ближняя к А), К (МК перпендикулярно AD), L, N. Ясно, что MKLN - прямоугольник, и KL = NM = FG = x. Обозначим так же точки касания окружностей с боковыми сторонми P (на АВ) и Q (на CD). Для простоты записи обозначим АМ = АР = y; BP = BN = z; CL = CQ = u; DL = DN = v; получаем
y + z = 13;
u + v = 15;
(y + u + x) + (z + v + x) = 2*21;
2*x = 2*21 - (13 + 15) = 14;
x = 7;
Вот теперь - как эту задачу можно решить моментально :))
Зададим вопрос - "на сколько надо сдвинуть центры обеих окружностей, чтобы они совпали?". После этой варварской операции получается описанная трапеция с боковыми сторонами 13 и 15 и основаниями a и b, причем,
a + b = 13 + 15; и
(a + b)/2 = 21 - x;
откуда x = 7;
Рассмотрим произвольный равнобедренный треугольник ABС с основанием BC, на боковой стороне которого как на диаметре построена окружность O(O;A). Допустим, что основание этого треугольника пересекает окружность в точке H. Докажем, что СH = BH. Соеденим вершину A с точкой H отрезком AH. Этот отрезок будет являться высотой, проведённой к основанию данного треугольника ( <AHB - вписанный угол по определению, притом он опирается на дугу, концы которой соединяет диаметр, т.е. на полуокружность, а значит, его градусная мера равна 90 гр., откуда отрезок AH - высота по определению). Но высота, проведённая к основанию равнобедренного треугольника также является и медианой, т.е. СH = BH, что и требовалось доказать.
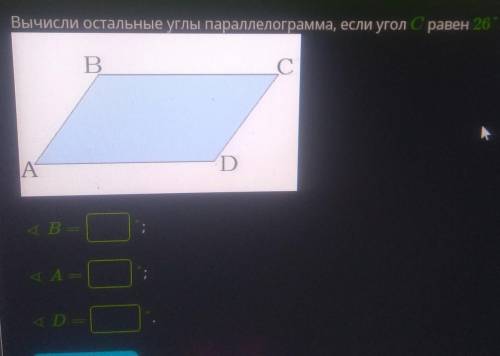
A=26°,B=154°, D=154°
Противоположные углы параллелограмма равны, а сумма соседних равна 180°
В=180-26=154°
B=D