Пусть Большее основание равно а, а меньшее- b, тогда
а=b+2*х, где х - отрезок между высотой, проведенной из вершины при меньшем основании к большему.
Через это уравнение находишь х.
Далее рассмотри треугольник между высотой боковой стороной трапеции и х
Высота- это расстояние между основаниями, и ее можно найти по теореме Пифагора
h(высота) = корень из (с^2(боковая сторона) - х^2)
h = sqrt(16-9)
h = sqrt(7)
HA = 6 см
КА = 6√2 см
КВ = 12 см
НВ = 6√3 см
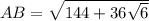 см
см
Объяснение:
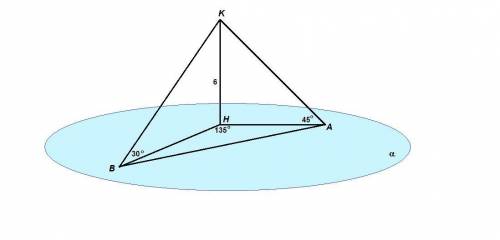
Проведем KH⊥α. Тогда КН = 6 см - расстояние от точки К до плоскости α.
Угол между прямой и плоскостью - это угол между прямой и ее проекцией на эту плоскость.
НА - проекция КА на плоскость α, значит ∠КАН = 45°,
НВ - проекция КВ на плоскость α, значит ∠КВН = 30°.
∠АНВ = 135°.
ΔКНА: ∠КНА = 90°, ∠КАН = 45°, значит треугольник равнобедренный,
НА = КН = 6 см
КА = 6√2 см как гипотенуза равнобедренного прямоугольного треугольника.
ΔКНВ: ∠КНВ = 90°,
КВ = 2КН = 12 см по свойству катета, лежащего против угла в 30°,
по теореме Пифагора:
НВ = √(КВ² - КН²) = √(144 - 36) = √108 = 6√3 см
Из ΔАНВ по теореме косинусов:
АВ² = НА² + НВ² - 2·НА·НВ·cos∠AHB
cos135° = cos(180° - 45°) = - cos45° = √2/2
AB² = 36 + 108 + 2 · 6 · 6√3 · √2/2 = 144 + 36√6
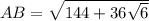 см
см
Заданная сторона АВ, О - точка пересечения медиан, S - площадь треугольника АВС.
Тогда площадь треугольника АОВ равна S/3,
а стороны АО = 18*(2/3) = 12, ВО = 24*(2/3) = 16, АВ = 20.
Очевидно, что АОВ - "египетский" треугольник (то есть прямоугольный треугольник, подобный треугольнику со сторонами 3,4,5, коэффициент подобия равен 4), поэтому его площадь равна 12*16/2 = 96, а площадь АВС S = 96*3 = 288
Что вы там у Гоши68 нашли неправильного? Все он верно сделал, просто написал без пояснений. Другое дело, что можно было бы заметить, что АОВ - прямоугольный треугольник, но и без этого все равно решение верное.
Вообще-то, я хочу пару слов сказать тут тем, кто серьезно готовится к экзаменам. Если вы применяете такую вещь, как формула Герона - вы должны быть готовы на ходу её вывести, если преподаватель потребует. И не только её, а еще и кучу сопутствующих формул вроде малоизвестной теоремы тангенсов ... А это намного сложнее и длинее, чем эта детская задачка.
Нам дана трапеция, следвательно стороны 5 и 11 параллельны. Расстоянием между двумя прямыми называют перпендикуляр проведенный от одной прямой к другой. Проведем две и у нас получится два прямоугольник треугольника и прямоугольник. т.к. верхняя сторона основания равна 5, то противоположная сторона фигуры тоже равна 5, далее 11-5 = 6, 6: 2=3 (т.к. два треугольника) и по теореме пифагора сторона равна корень из 7