
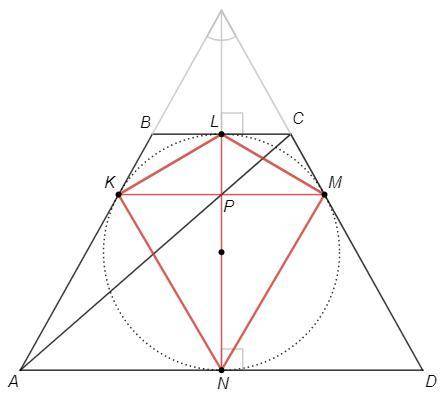
Достроим трапецию до равнобедренного треугольника.
Центр вписанной окружности лежит на биссектрисе.
Биссектриса к основанию является высотой и медианой.
Окружность касается оснований в серединах.
BL=CL, AN=DN
Отрезки касательных из одной точки равны.
BK=BL=CL=CM =a
AK=AN=DN=DM =b
По теореме о пропорциональных отрезках KM||BC||AD
△KAP~△BAC, KP/BC=AK/AB => KP/2a =b/(a+b)
△PCM~△ACD, PM/AD=CM/CD => PM/2b =a/(a+b)
KP=PM =2ab/(a+b)
LN - высота => LN⊥KM
S(KLMN) =1/2 KM*LN *sin90 =2ab/(a+b) *LN
S(ABCD) =1/2 (AD+BC)*LN =(a+b) *LN
S(ABCD)/S(KLMN) =(a+b)^2/2ab =8/3 =>
(a^2 +b^2 +2ab)/2ab =8/3 =>
a/2b +b/2a +1 =8/3 =>
a/b +b/a =2(8/3 -1) =10/3
a/b =x
x +1/x =10/3 =>
x^2 -10/3 x +1 =0 => x = {1/3; 3}
ответ: основания относятся 1:3
ответ: переведено с программы-переводчика, русская оригинальная версия в объяснении
(Точка М на малюнку відповідає точці E в даній задачі)
Так як бісектриса кута паралелограма відсікає від нього рівнобедрений трикутник, то АВ = ВЕ = 7 см
У параллелограмме всі сторони попарно рівні і паралельні.
З цього випливає, що AD = ВС = 12 см
ЕС = ВС - ВЕ = 12 - 7 = 5 см
Відповідь: BE = 7 см і EC = 5 см
Объяснение:
(Точка М на рисунке соответствует точке E в данной задаче)
Так как биссектриса угла параллелограмма отсекает от него равнобедренный треугольник, то АВ = ВЕ = 7 см
В параллелограмме все стороны попарно равны и параллельны.
Из этого следует, что AD = ВС = 12 см
ЕС = ВС - ВЕ = 12 - 7 = 5 см
ответ: BE = 7 см и EC = 5 см

2.) AD паралельно BC,тогда угол DAE равен углу DEA, AE бессектриса угла BAD и угол DAE равен углу BAE,то угол BEA равен углу BAE,отсюда треугольник BAE равнобедренный и AB=BE =36
AB=DC=36°,BC+AD=P - AB-CD=96 см, так как AD=BC то AD = BC = 96:2= 48 см
Сторона АD 48 см