Рассмотрим прямоугольник со сторонами a, b и площадью S.
Докажем, что S = ab.
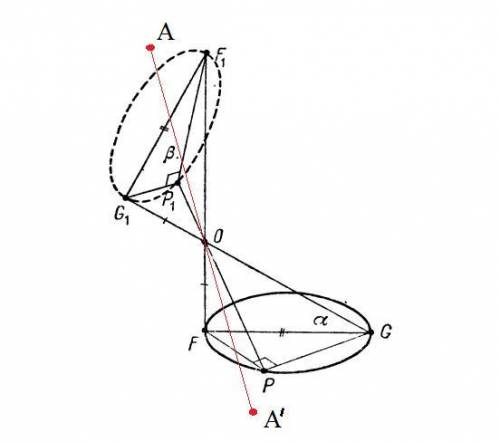
Достроим прямоугольник до квадрата со стороной a + b, как показано на рисунке 1.
Так как площадь квадрата равна квадрату его стороны, то площадь этого квадрата равна (a + b)2.
С другой стороны, этот квадрат составлен из данного прямоугольника с площадью S, равного ему прямоугольника с площадью S (так как, по свойству площадей, равные многоугольники имеют равные площади) и двух квадратов с площадями a2 и b2. Так как четырехугольник составлен из нескольких четырехугольников, то, по свойству площадей, его площадь равна сумме площадей этих четырехугольников:
(a + b)2 = S + S + a2 + b2, или a2 + 2ab + b2 = 2S + a2 + b2.
Отсуда получаем: S = ab, что и требовалось доказать.
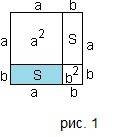
Соединив точки А и Р, получим прямоугольную трапецию АРСД.
Диаметр вписанной в трапецию окружности равен ее высоте, здесь - стороне АВ=СД, т.е. 4. Радиус r=2 см
Проведем из центра О радиусы в точки касания окружности с ВС и СД. Отрезки касательных, проведенные из одной точки, равны.
КС=СЕ=r=2 см.
ВК=ВС-КС=5-2=3 см
Обозначим М середину АВ, Е - середину СД.
МО=ВК=3 см
АМ=СЕ=ДЕ=4:2=2 см
По т.Пифагора или как гипотенуза равнобедренного ∆ ОЕД –
ОД=2√2.
Р (АМОД)=АД+АМ+МО+ОД=5+2+3+2√2=(10+2√2) см или ≈ 12, 828 см