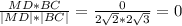Шаг 1. Поставить острие циркуля в вершину угла и на обоих лучах угла отложить равные отрезки (сделать засечки) . Шаг 2. Не меняя раствора циркуля поставить поочередно острие циркуля на засечки, сделанные в шаге 1, и провести дуги, так, чтобы они пересеклись. Шаг 3. Точку пересечения дуг соединить с вершиной угла. Это и будет биссектриса. Объяснение. Если соединить засечки, сделанные на шаге 1 с точкой пересечения дуг, то получится ромб. Диагональ ромба является биссектрисой его противоположных углов.
1) BM≈10
2)cosα=0
Объяснение:
1)Дано трикутник ABC
A(0;-3;-1)
B(-4;0;2)
С(8;3;-7)
BM-медіанна
AC(8-0;3-(-3);-7-(-1)) AC(8;6;-6)
М-середина AC
M(8/2;6/2;-6/2) M(4;3;-3)
BM(4-(-4);3-0;-3-2) BM(8;3;-5)
|BM|=√(8²+3²+(-5)²)=√(64+9+25)≈10
2)M(0;1;-1) B(1;-1;2) C(3;1;0) D(2;1;1)
MD(2-0;1-1;1-(-1)) MD(2;0;2)
BC(3-1;1-(-1);0-2) BC(2;2;-2)
Знайдемо скалярний добуток векторів:
MD·BC=2·2+02+2·(-2)=4+0-4=0
Знайдемо довжини векторів:
|MD|=√(2²+0²+2²)=√(4+0+4)=√8=2√2
|BC|=√(2²+2²+(-2)²)=√(4+4+4)=√12=2√3
Знайдемо кут між векторами:
cosα=