
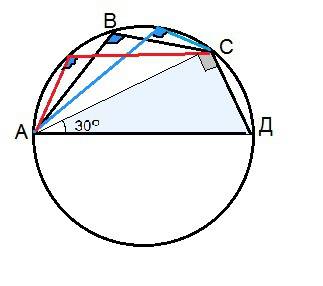
Сторона АД, четырехугольника АВСД - диаметр окружности по условию.
Треугольник АСД - прямоугольный, т.к. угол АСД опирается на диаметр окружности и равен половине стягиваемой диаметром дуги (по свойству вписанного угла).
Отсюда угол СДА равен 180º-90º-30º=60º.
Известно, что вокруг четырехугольника можно описать окружность, только тогда, когда сумма его противоположных его углов равна 180 градусов.
Мы нашли, что угол Д равен 60º, поэтому противолежащий ему угол В равен 180ª-60ª=120º. И где бы ни находилась вершина В четырехугольника АВСД, угол АВС будет опираться на одну и ту же дугу, стягиваемую хордой АС - дугу АДС, и будет равен 120 градусам.
Нарисуем прямоугольный треугольник и окружность в нем.
Не обязательно точно, но чтобы иметь представление, о чем речь.
Вспомним свойство касательных, проведенных из точки к окружности.
От прямого угла откладываем 6 см в обе стороны на двух катетах.
Далее от одного из острых углов тоже по обе стороны от вершины откладываем 10см.
Отрезки касательных у третьей вершины обозначим х.
У нас есть
катет 6+10=16
второй катет 6+х
гипотенуза 10+х
Составим уравнение гипотенузы по теореме Пифагора.
(10+х²)=(6+х)²+16²
100+20х+х²=36+12х+х²+256
100+20х =36+12х +256
20х-12х=192
х=24
Периметр равен
2(10+6+24)=80см