27:5
Объяснение:
Проведем высоты трапеции DP и СК.
Тогда по т. Пифагора АР^2=AD^2-DP^2
Поскольку радиус вписанной окружности =6, то DP=12 см
AP^2= 225-144=81
AP=9 cm
Аналогично CK=5 cm
Поскольку ABCD четырехугольник, описанный вокруг окружности, то
AB+CD=AD+CB=28
2*CD+AP+KB=28
2*CD+9+5=28
2*CD=14
CD=7 cm AB=21 cm
Пусть R точка пересечения диагоналей трапеции.
Треугольники АОВ и СОD подобны ( по 2-м углам- углы BDC и DBA -накрест лежащие, Значит равны. Аналогично ACD=CAB)
Тогда AB/DC= AR/CR=BR/DR= 3/1
=>DB:DR=4:1 AC:RC=4:1
Треугольники MDR и ADR тоже подобны ( по 2- м углам DMR=DAB- соответствующие углы при параллельных прямых)
Тогда AB/MR=BD/RD=4:1
=>MR=AB/4=21/4
Пусть точка Z - точка пересечения DP и МН .
Тогда из подобия треугольников MDR и ADR следует, что DZ/DP=1/4
=> DZ=12/4=3 PZ=9
Аналогично треугольники АСВ и RCH тоже подобны
RH=AB/4 =21/4 => MH=MR+RH=21/2
Теперь выразим площади АМНВ и MDCH
S(AMHB)= (AB+MH)*PZ/2
S(MDCH)=(MH+DC)*DZ/2
Тогда:
S(AMHB):S(MDCH)= (AB+MH)*PZ/((MH+DC)*DZ)=
(21+21/2)*9/((21/2+7)*3)= 63*3/35=9*3/5 = 27:5
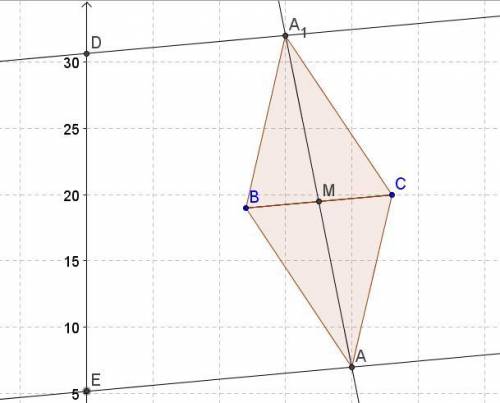
Даны координаты точек B (12,19), C (23,20) и A (p, q).
Площадь треугольника АВС равна 70 кв.ед.
Угловой коэффициент медианы АМ равен -5.
Находим уравнение прямой ВС и длину отрезка ВС.
|ВС| = √((23-12)² + (20-19)²) = √(11² + 1²) = √122.
BC: (x - 12)/11 = (y - 19)/1, х - 12 = 11у - 209.
Уравнение ВС: х - 11у + 197.
Теперь найдём высоту треугольника АВС:
h = 2S/|AB| = 2*70/√122 = 140/√122.
Точка А лежит на прямой, параллельной ВС и отстоящей выше или ниже на расстоянии h.
Так как точка принадлежит медиане АМ, находим координаты точки М - середины отрезка ВС.
М((12+23)/2); (19+20)/2) = ((35/2); (39/2)).
Уравнение медианы через точку М в виде у = кх + в. Подставим координаты точки М. 39/2 = -5*(35/2) + в,
отсюда в = (39/2) + (175/2) = 214/2 = 107.
Уравнение АМ: у = -5х + 107 или у + 5х - 107 = 0.
Уравнение прямой, удаленной на расстояние h от исходной имеет вид: Ax + By + C ± h√(A² + B²).
Подставим коэффициенты уравнения ВС (для параллельных прямых они сохраняются).
АЕ = х - 11у + 197 - (140/√122)*√(1² + 11²) = х - 11у + 57.
А1Д = х - 11у + 197 + (140/√122)*√(1² + 11²) = х - 11у + 337.
Координаты точек А и А1 находим как точки пересечения прямых.
х - 11у + 337 = 0 (х-5), -5х + 55у - 1685 = 0
5х + у - 107 = 0, 5х + у - 107 = 0
56у = 1792 у = 1792/56 = 32.
х = 11*32 - 337 = 15.
Точка А1(32; 15). Аналогично для А.
х - 11у + 57 = 0 (х-5), -5х + 55у - 285 = 0
5х + у - 107 = 0, 5х + у - 107 = 0
56у = 392 у = 392/56 = 7.
х = 11*7 - 57 = 20.
Точка А(20; 7).
ответ: 2 значения p+q = 27 и 47.
ответ на фото:) слеоай ответ лучшим если не сложно