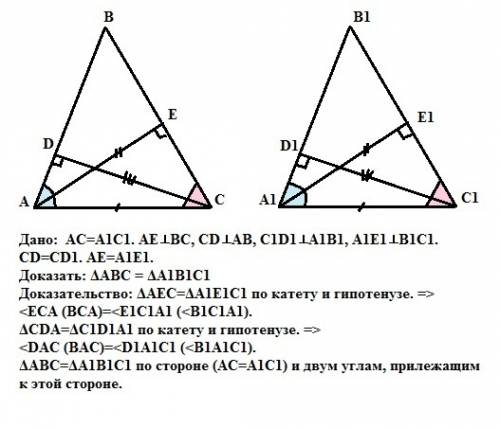
Пусть даны треугольники АВС и А1В1С1, у которых стороны АС и А1С1 равны. Высоты, проведенные из концов этих сторон к боковым сторонам треугольников, также равны. То есть АЕ = А1Е1 и СD = C1D1. Прямоугольные треугольники АЕС и А1Е1С1, ADC и A1D1C1 равны по катету и гипотенузе (четвертый признак равенства прямоугольных треугольников) так как АС=А1С1 (гипотенуза), а АЕ=А1Е1 и CD=C1D1 (катеты) - дано.Из этого равенства следует равенство углов DAC и D1A1C1, а также углов АСЕ И А1С1Е1. Тогда треугольники АВС и А1В1С1 равны по второму признаку равенства треугольников, так как у них равны стороны (АС=А1С1) и углы, прилежащие к этим сторонам (<ВАС = <В1А1С1 и <ВСА=<В1А1С1 - доказано выше).
Что и требовалось доказать.
ВК=2, АК=8, тогда, АВ=10.
Центр вписанной окружности лежит в точке пересечения биссектрис треугольника, проведём биссектрису ВН: точка Н совпадёт с точкой касания окружности на стороне АС, т.к. в биссектриса, проведённая из угла В, является и высотой, и медианой, т.е. угол АНС = 90 градусов.
АН=АК, т.к. отрезки касательных, проведённых из одной точки, равны, т.е. АН=8, тогда АС=16.
В прямоугольном треугольнике АВН АВ=10, АН=8, тогда по теореме Пифагора ВН=6.
Найдём площадь треугольника: 1/2 * АС * ВН = 1/2 * 16 * 6 = 42.