ответ: 22см, 24см, 44см
Объяснение:
Пусть одна сторона треугольника=х, тогда вторая=х+2, а третья=2х и, зная, что периметр=90см, составим уравнение:
х+х+2+2х=90
4х=90–2
4х=88
х=88÷4=22
Итак: первая сторона=22см, тогда 2-я сторона=22+2=24см, а 3-я сторона=2×22=44.
Проверка:
Р=22+24+44=90см
Задача 1.
S=kh
Соответственно k=S:h
60:12=5 - средняя линия трапеции
Задача 2.Площадь трапеции вычисляется по формуле a+b/2*h подставляем известные нам значения в формулу получаем 8*(8+b/2)=72
=128+b=144
b=16
Задача 3.
S=kh
Соответственно k=S:h
63:7=9 - средняя линия трапеции
Задача 4.
12*1+b/2=60
1+b=5
b=4
Задача 5
рассмотрим треугольник, образованный высотой, опущенной на основание и наклонной боковой стороной. Он прямоугольный и равнобедренный. Значит высота трапеции равна разнице между основаниями 9-5=4
площадь равна высоте умноженной на полусумму оснований 4 * (9+5)/2 =28
Первое решение полное и понятное. Если не помните формулу Герона, есть
Вариант решения ( без формулы Герона).
Формула радиуса описанной окружности
R=a•b•c/4S, где а, b, и с - стороны треугольника
S-a•h
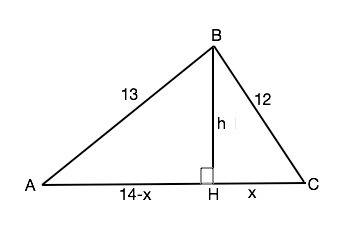
Проведем к большей стороне АС высоту ВН.
Примем СН=х
Тогда АН=14-х
По т.Пифагора
ВН²=АВ²-АН² =169-196+28х-х²
ВН²=ВС²-СН²=144-х²
Приравняем значения квадрата высоты:
169-196+28х-х²=144-х², откуда
28х=171
х=6,107
ВН=√(144-37,3)=√106,7=10,33
S=10,33•14/2=72,31
R=12•13•14/4•72,31=546/72,3= ≈7,55 см
sinA=BH/АВ==10,33/13= ≈0,7946
∠А≈52°36'
внизу
Объяснение:
Пусть меньшая сторона равна х, тогда, поскольку она меньше другой, другая х+2, а третья 2х. Периметр=х+х+2+2х=90 см. ⇒ 4х=88 см, ⇒ х=88:4=22 см; х+2=24 см, 2х=44 см. (22+24+44=90)