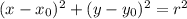 , где r - радиус,
, где r - радиус, 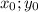 - координаты центра окружности. Из данных уравнений следует, что координаты центра первой окружности (-3;1), или х1=-3, у1=1, а второй - (2;-2), или х2=2, у2=-2. Уравнение прямой можно составить, зная две точки этой прямой, по формуле:
- координаты центра окружности. Из данных уравнений следует, что координаты центра первой окружности (-3;1), или х1=-3, у1=1, а второй - (2;-2), или х2=2, у2=-2. Уравнение прямой можно составить, зная две точки этой прямой, по формуле: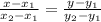
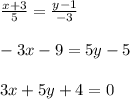
В каждой вершине параллелепипеда сходятся смежные стороны трех граней, и их диагонали образуют треугольник. (см. рисунок вложения)
В данном случае диагонали равны 30, 40 и 70 см.
По теореме о неравенстве треугольников: длина любой стороны треугольника меньше суммы длин двух других сторон.
Здесь имеем "треугольник" и три длины, и 70=30+40.
Тогда меньшие стороны "лягут" на большую, и треугольник не получится, как и параллелепипед с такими диагоналями граней.
Не могут диагонали трех граней прямоугольного параллелепипеда иметь длины 30 см, 40 см и 70 см.