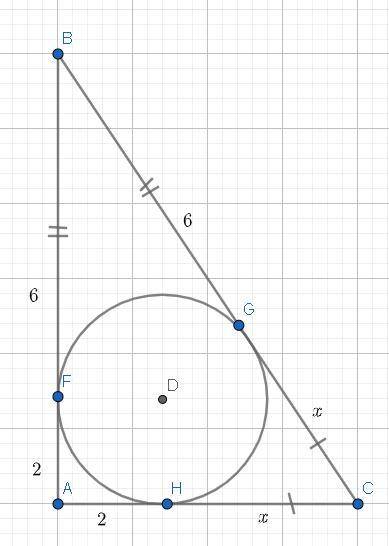
В случае окружности, вписанного в прямоугольный треугольник — точки касания делят все стороны на некие равные отрезки.
То есть: Через точку B — проведены 2 касательные: катет BA & гипотенуза BC.
В точках касания — отрезки друг другу равны(теорема о 2 касательных, проведённых с одной точки), тоесть: BF == BG.
BF == BG ⇒ BF == BG = 6.
Одни и те же действия с отрезками FA & AH, они тоже друг другу равны, так как их касательные проведены с одной точки.
FA == AH = 2.
Точно так же с отрезками HC & GC: HC == GC = x.
По теореме Пифагора:
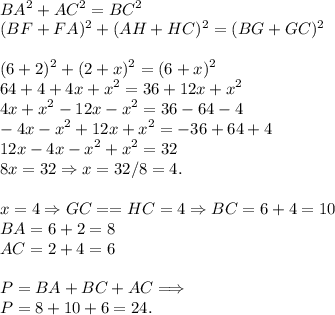
Вывод: P = 24 см.
БРАВЛ СТАРС
─────────────────────────────
────────────▄████▄───────────
───────────▄██████▄──────────
───────────█──────█──────────
───────────█──────█──────────
───────────█─▄▄▄▄─█──────────
───────────█──────█──────────
───────────█──────█──────────
───────────█─▄▄▄▄─█──────────
───────────█──────█──────────
───────────█──────█──────────
───────────█─▄▄▄▄─█──────────
───────────█──────█──────────
───────────█──────█──────────
───────────█─▄▄▄▄─█▄▄▄▄──────
────▄███████──────█▀█─▀██▄───
▄█████─────█──────█──█─▀██▄──
█────█─────█──────█───█──██▄─
█────█─────█──────█────█──██▄
█────█─────█──────█─────█──██
█────█─────█──────█─────█─██▀
█────█─────█──────█─────███▀─
█────█─────█──────█─────██▀──
█───────────────────────██───
███▄────────────────────█▀───
─▀███▄────────────────▄██────
───▀████████████████████▀────
─────▀████████████████▀──────
────────▀███████████▀────────
ак, начнем с того, что нарисуем треугольник. АВ=ВС=12, 8 см;
к основанию АС проведём высоту ВН (и она же является медианой).
Площадь треуг. АВС=1/2*ВН*АС
Рассмотрим треуг. АНВ: он прямоугольный, т.к. угол ВНА=90 градусов.
По свойству угла в 30 градусов (угол ВАН) ВН=АВ/2=12,8 см/2=6,4 см.
АН=СН, а АС=2АН. По теореме Пифагора АН= корень квадратный из выражения:
(12,8 см) в квадрате минус (6,4 см) в квадрате; АН= корень кватратный из (12,8*12,8 - 6,4*6,4).
АН приближенно равна 11,1 см.
АС=2*11,1 см=22,2 см.
Площадь треуг. АВС= 1/2*6,4 см*22, 2 см= 71 квадратный см.
Можно и по формуле Герона найти (вычислив предварительно полупериметр).