
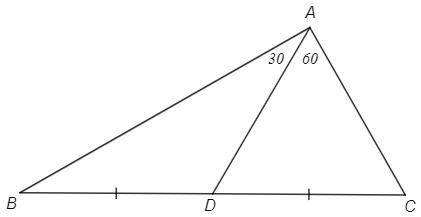
BAC =BAD +CAD =30+60 =90
Медиана из прямого угла равна половине гипотенузы, AD=BD
△ADB - равнобедренный, B=BAD=30
В треугольнике (ABC) с углами 30, 60, 90 стороны относятся как 1:√3:2
AC=AB/√3 =1
----------------------------
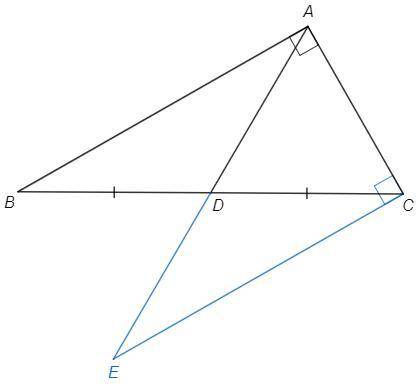
Докажем.
Продлим AD на равный отрезок, DE=AD.
△EDC=△ADB (по двум сторонам и углу между ними)
AB||CE (по накрест лежащим), AB⊥AC => CE⊥AC
△CEA=△ABC (по двум катетам) => AE=BC => AD=DE=BD=DC
(Медиана из прямого угла равна половине гипотенузы.)
△DAC - равносторонний (равнобедренный с углом 60), AC=DC.
(Катет против угла 30 равен половине гипотенузы.)
AC=x, BC=2x
По теореме Пифагора: AB =√(BC^2-AC^2) =x√(4-1) =x√3
AC:AB:BC = 1:√3:2
Опуская перпендикуляры из Н к катетам основания-получаю НН1 и НН2.
С высотой пирамиды НS они образуют прямоугольные треугольники.
В этих треугольниках SH-общая высота и одинаковый угол бетта по условию.
Учитывая что высота в них может быть выражена SH=HH1*tgβ=HH2tgβ-следует
что НН1=НН2.
Теперь надо выразить это НН1 через а и ∠α. Н делит гипотенузу на две части b и a-b, выражу b через а...-второй рисунок
Высота пирамиды HS=HH1*tg β=a*sinα*cosα*tgβ/(sinα+cosα)
Площадь основания S(осн)=a^2*sinα*cosα/2
Тогда объем пирамиды V=S(осн)*SH/3=a^3*sin^2(2α)*tgβ/(24(sinα+cosα))