Объяснение:
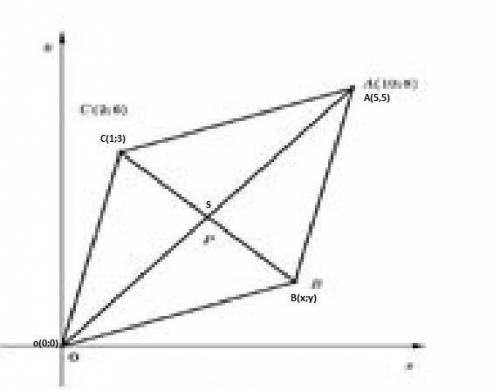
Вычисляем центр диагонали 0А по формуле
: S=(XB+XA)/2 ; (YB+YA)/2
S(OA)=(0+5)/2 ; (5+0)/2 = (5/2;5/2) = (2,5 ; 2,5)
Рассчитаем центр диагонали BО
S(BC)=(1+xB)/2 ; 3+yB)/2
* мы заменяем x и y на x и y z S(OA) (5/2;5/2)
(1+xB)/2=2,5 I *2 ; (3+yB)/2=2,5 I* 2
1+xB=5 3+yB=5
xB=5-1 yB=5-3
xB=4 yB=2
OTBET: Точка поиска B = (4; 2)
(w załączeniu grafik)
Дано:
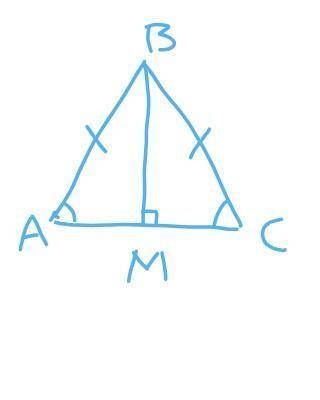
треугольник АВС,
угол А = угол С,
ВМ — высота.
Доказать: треугольник АВМ = треугольник СВМ.
Доказательство:
Свойство равнобедренного треугольника: если в треугольнике два угла равны, то этот треугольник является равнобедренным.
(У нас, по условию задачи, угол А равен углу С, значит треугольник АВС является равнобедренным)
угол А = угол С => треуг. АВС — равнобедренный.
(Равнобедренный треугольник — треугольник, у которого две стороны равны, эти две стороны называются боковыми сторонами, а третья сторона — основанием. Какие же стороны боковые? Признак равнобедренного треугольника: если треугольник является равнобедренным, то углы при его основании равны. Соответственно, сторона АС является основанием, а стороны АВ и ВС — боковые стороны и они равны)
АВ = ВС.
(Теперь разберёмся с высотой ВМ. Высота равнобедренного треугольника — перпендикуляр, проведённый из вершины треугольника, к противолежащей стороне, в данном случае, к основанию треугольника)
ВМ — высота, ВМ перпендикулярно АС. <рисунок1>
Свойство равнобедренного треугольника: в равнобедренном треугольнике медиана, биссектрисса и высота, проведённые из вершины, противолежащей основанию, совпадают.
(Получается, высота ВМ — это и биссектрисса ВМ, и медиана ВМ. Биссектриса — прямая, делящая угол пополам. Медиана — отрезок, соединяющий вершину треугольника с серединой противоположной стороны, в данном случае, с серединой основания)
Рассмотрим ВМ как биссектрису => угол АВМ = угол СВМ. <рисунок2>
Рассмотрим ВМ как медиану => АМ = МС. <рисунок3>
(Соединим все полученные данные и докажем, что треугольники АВМ и СВМ равны. По всем трём признакам равенства треугольников, эти треугольники равны, но распишем третий признак)
Третий признак равенства треугольников — по трём сторонам: если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
АВ = ВС, ВМ — общая сторона для двух треугольников, АМ = МС => треугольник АВМ = треугольник СВМ.
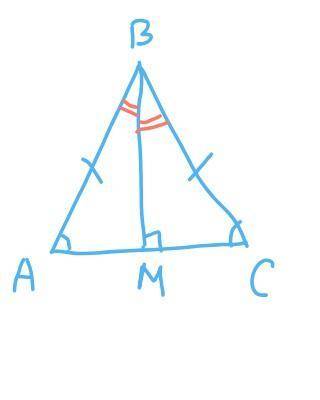

Получается, что Б
1500 больше 300 в 5 раз