Дано:
усеченный конус
r = O₁B = 5 см
R = OA = 11 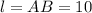см
см
-----------------------------
Найти:
Sсеч - ?
1) Проведем BH⊥AO.
OH = O₁B = r = 5 см
AH = OA - OH = R - r = 11 см - 5 см = 6 см
2) Рассмотрим ΔAHB:
BH⊥AO | ⇒ ΔAHB - прямоугольный
∠AHB = 90° |
AB² = AH² + HB² - по теореме Пифагора, следовательно: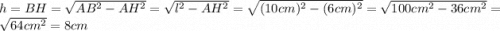
h = BH = OO₁ = 8 см
3) Равнобедренная трапеция ABCD является осевым сечением данного усеченного конуса: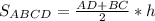 
4) В трапеции ABCD:
AD = 2AO = 2R = 2×11 см = 22 см h = BH= 8 см
BC = 2BO₁ = 2r = 2×5 см = 10 см
5) Тогда площадь трапеции равна:
⇒
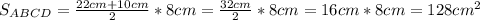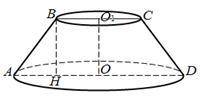
Sсеч =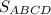 
= 128 см²
ответ: Sсеч = 128 см²
P.S. Рисунок показан внизу↓
y = 2sinx + 1
Объяснение:
На рисунке изображен график функции y = 2sinx + 1
График функции y = sinx сдвинут относительно оси Y на +1 единицу, коэффициент растяжения вдоль оси Y = 2.
Свойства функции y = 2sinx + 1.
Функция y = 2sinx + 1 периодическая, период T = 2π
Ось Y пересечена в т.(0; 1 ):
x = 0; y = 2*sin0 + 1 = 2 * 0 + 1 = 1
Нули функции:
y = 0; 2sinx+1 = 0; sinx = -1/2
x₁ = arcsin(-1/2) + 2πn = 7π/6 + 2πn; n∈Z
x₂ = π - arcsin(-1/2) + 2πn = π - 7π/6 + 2πn = -π/6 + 2πn; n∈Z
Максимальное значение функции y = 2 * 1 + 1 = 3 (т.к. максимальное значение функции sinx = 1)
Минимальное значение функции y = 2 *(-1) + 1 = -2 + 1 = -1 (т.к. минимальное значение функции sinx = -1).