Имеем два подобных треугольника с соответственными сторонами 9,8м и 0,8 м; 1,2м и х. Составим и решим уравнение 9,8/0,8=х/1,2. х=14,7 или 15м.
Медианы треугольника пересекаются в одной точке.
Высоты треугольника пересекаются в одной точке.
В данном треугольнике эти точки совпадают - медианы являются также высотами.
Совпадение медианы и высоты к основанию - признак равнобедренного треугольника.
Таким образом данный треугольник является равнобедренным относительно любой стороны, то есть равносторонним.
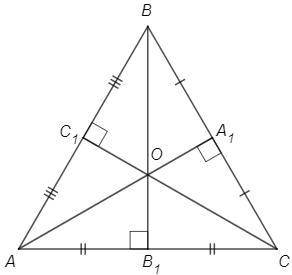
O - точка пересечения медиан, AA1 - медиана, A1 - середина BC.
O - точка пересечения высот (ортоцентр), AA1 проходит через точку O => AA1 - высота, AA1⊥BC
∠AA1B=∠AA1C=90 (AA1 - высота)
BA1=CA1 (AA1 - медиана)
△BAA1=△CAA1 (по двум катетам, AA1 - общий) => AB=AC
(Доказали: Если медиана треугольника совпадает с его высотой, то треугольник равнобедренный.)
Аналогично: BB1 - медиана и высота к стороне AC => AB=BC
AB=AC=BC, △ABC - равносторонний
Следует воспользоваться признаками подобия треугольников. Если построить прямоугольный треугольник, то 1катет=1,2м 2катет=0,8м а нипотенуза=9,8м. Т.к. это прямоугольный треугольник то 1катет- это высота а отсюда следует, чтто высота=1катету, т.е. 1,2м