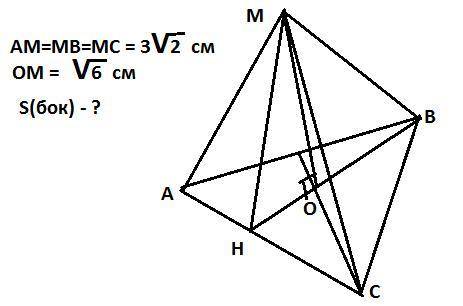
ответ: S(бок) - 27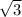
см²
Объяснение:
Надо вычислить апофему и сторону основания.
1. Найдем апофему.
В правильной треугольной пирамиде, высота падает на точку пересечения медиан (в центр вписанной окружности, но в этом случае он совпадает с точкой пересечения медиан и это облегчает задачу).
Найдем отрезок медианы ОВ:
ОВ^2 = MB^2 - MO^2 = 18-6 =12
Тогда ОВ = 2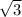 см. Прямо отсюда видно, что ОМ =
В точке пересечения медиана делится в соотношении 2:1 начиная от вершины, поэтому ОВ =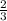 
ВН, отсюда ВН = 
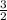ОВ =
Значит отрезок ОМ = 4,5-3=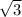 см
Из треугольника МОН апофема будет МН^2=OH^2 +OM^2 = 6+3 = 9
МН= 3 см
2. Найдем сторону. Медиана ВН делит сторону пополам (обозначим сторону а) . С учетом этого из прямоугольного треугольника АВН
a^2 - (a/2)^2 = BH^2 или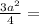 
27, тогда а= 6 см
Площадь одной грани
S₁ = 0,5*a*BH = 0,5*6*3*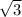 = 9
А всех трех
S(бок) = 3*S₁ = 3*9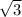 = 27
Объяснение:
Квадрат
Квадрат — это четырехугольник, имеющий равные стороны и углы.
Квадрат ABCD
Диагональ квадрата — это отрезок, соединяющий две его противоположные вершины.
Параллелограмм, ромб и прямоугольник так же являются квадратом, если они имеют прямые углы, одинаковые длины сторон и диагоналей.
Свойства квадрата
1. Длины сторон квадрата равны.
AB=BC=CD=DAAB=BC=CD=DA
Квадрат с равными сторонами
2. Все углы квадрата прямые.
\angle ABC = \angle BCD = \angle CDA = \angle DAB = 90^{\circ}∠ABC=∠BCD=∠CDA=∠DAB=90
∘
Квадрат с прямыми углами
3. Противолежащие стороны квадрата параллельны друг другу.
AB \parallel CD, BC \parallel ADAB∥CD,BC∥AD
4. Сумма всех углов квадрата равна 360 градусов.
\angle ABC + \angle BCD + \angle CDA + \angle DAB = 360^{\circ}∠ABC+∠BCD+∠CDA+∠DAB=360
∘
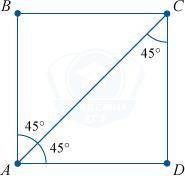
5. Величина угла между диагональю и стороной равна 45 градусов.
\angle BAC = \angle BCA = \angle CAD = \angle ACD = 45^{\circ}∠BAC=∠BCA=∠CAD=∠ACD=45
∘
Квадрат с диагональю и углами 45 градусов
Доказательство
6. Диагонали квадрата — тождественны, перпендикулярны и разделяются точкой пересечения пополам.
AO = BO = CO = DOAO=BO=CO=DO
\angle AOB = \angle BOC = \angle COD = \angle AOD = 90^{\circ}∠AOB=∠BOC=∠COD=∠AOD=90
∘
AC = BDAC=BD
Квадрат тождественными, перпендикулярными диагоналями
Доказательство
7. Каждая из диагоналей делит квадрат на два равнобедренных прямоугольных треугольника.
\triangle ABD = \triangle CBD = \triangle ABC = \triangle ACD△ABD=△CBD=△ABC=△ACD
8. Обе диагонали делят квадрат на 4 равнобедренных прямоугольных треугольника.
\triangle AOB = \triangle BOC = \triangle COD = \triangle AOD△AOB=△BOC=△COD=△AOD
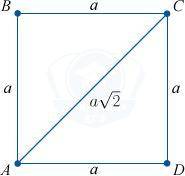
9. Если сторона квадрата равна a, то, диагональ будет равна a \sqrt{2}a√
2
.
Квадрат с диагональю равной a\sqrt2
Доказательство
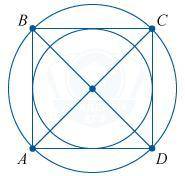
10. Центром квадрата, а так же вписанной в него и описанной окружности является точка пересечения диагоналей
Квадрат с диагоналями, вписанной и описанной окружностью
216 кв.см.
Объяснение:
AE=AB+BE;
50+10BE=15BE; 50=5BE; BE=10; AE=5+10=15
ED=EC+CD;
10EC+60=15EC; 60=5EC; EC=12; ED=6+12=18
Нашли длины всех трёх сторон треугольника: AE=15; ED=18;AD=15
В общем случае решения, для нахождения площади треугольника по трём сторонам, нужно использовать формулу Герона.
Но в нашем случае треугольник равнобедренный (AE=AD=15), поэтому найдём длину высоты на сторону ED по теореме Пифагора: