Пусть х м - длина основания равнобедренного треугольника, где x>0, тогда длина боковой стороны этого же равнобедренного треугольника по условию равна 12х м, т.к. периметр этого треугольника равен 10 м по условию, получаем уравнение:
х+12х+12х=10
25х=10
х=0,4
Значит, 0,4 м - длина основания.
ответ: 0,4 м.
Теорема Пифагора: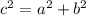 
, где с - гипотенуза, а а и b - катеты прямоугольного треугольника.
К равнобедренному треугольнику она не относится (исключение составляет если основание равнобедренного треугольника является гипотенузой прямоугольного треугольника, т.е. угол, лежащий против основания равнобедренного треугольника - прямой, т.е. равен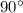 
).
так как боковые стороны равны, то трапеция равнобедренная, проведем две высоты в трапеции, расстояние между высотами и концами оснований равно (13-9)/2=2(см)
получим прямоугольный треугольник с известными двумя сторонами 4 и 2. Это прямоугольный треугольник, если в прямоугольном треугольнике катет равен половине гипотенузы, то угол лежащий против этого катета равне 30 градусов, угол трапеции равен сумме найденного угла и прямого угла, т. е 30+90=120, второй угол равен 180-120=60
ответ 120, 120, 60, 60