Соединяя середины сторон параллелограмма, мы получим параллелограмм, так как стороны получившегося четырехугольника (MNPQ - см. чертеж!) являются средними линиями ( MN - для ΔABC, NP - для ΔBCD и так далее), а значит MN ║ AC, QP ║ AC ⇒ MN ║ QP и, аналогично, MQ ║ BD, NP ║ BD ⇒ MQ ║ NP, но так как MNPQ - ромб (по условию), то по свойству средней линии: AC = BD (из равенства средних линий вытекает равенство сторон, которым они параллельны, так как стороны в 2 раза больше соответствующих средних линий)
Из равенства диагоналей параллелограмма следует, что он является прямоугольником (признак прямоугольника)

Для доказательства достаточно показать, что один из углов, например, угол С прямой. Тогда все углы параллелограмма будут прямыми и получится прямоугольник.
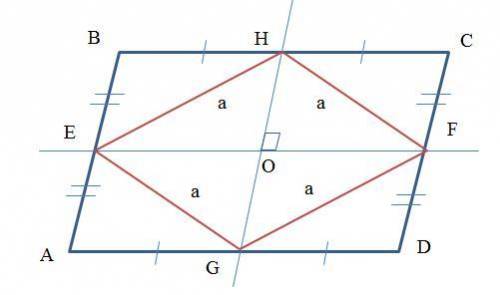
Пусть E, F, G и H середины сторон параллелограмма (см. рисунок).
Через пару точек E и F, G и H проведём прямые. Так как точки E и F, G и H середины сторон параллелограмма, то прямые EF || BC и GH || CD.
С другой стороны отрезки EF и GH являются диагоналями ромба EHFG и поэтому пересекаются под прямым углом, то есть EF⊥GH. Но EF || BC и GH || CD, откуда следует, что BC⊥CD, что и требовалось доказать.
ответ: 20 см
Решение: смотри рисунок.
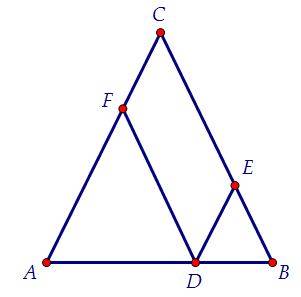
Пусть треугольник BAC равнобедренный, AB=AC=10 см.
Возьмем произвольную точку K на основании BC и проведем KM||AC иKN||AB
KM=AN, KN=AM -противоположные стороны параллелограмма.
Докажем, что KM=BM. Угол 2=углу 4 как соответственные углы при AC||KM и секущей KC. Но угол 4=углу 1 (углы при основании равнобедренного треугольника). Отсюда угол 2=углу 1. Значит треугольник BMK равнобедренный и KM=BM как его боковые стороны.
Аналогично докажем, что KN=NC. Угол 3=углу 1 как соответственные углы при AB||KN и секущей KB. Но угол 1=углу 4 (углы при основании равнобедренного треугольника). Отсюда угол3 =углу 4. Значит треугольник KNC равнобедренный и KN=NC как его боковые стороны.
Периметр параллелограмма =KM+MA+AN+NK=BM+MA+AN+NC=BA+AC=10+10=20 (см)
Дополнительное построение диагонали параллелограмма AC и BD
по условию вершины ромба являются серединами сторон параллелограмма, значит стороны ромба равны 1/2 диагоналей (AC и BD) параллелограмма (из свойств средней линии тр-ка)
а так как в ромбе все стороны равны значит и диагонали параллелограмма равны.
а следовательно этот параллелограмм прямоугольник