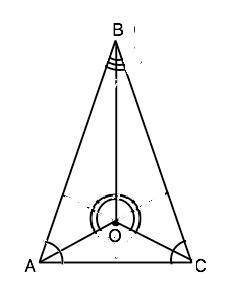
О - точка пересечения биссектрис треугольника АВС.
∠AOB = ∠COB. Найти наименьший угол треугольника ABC, если ∠ABC в три раза меньше ∠AOC
ответ: 36°
Объяснение:
ВО- биссектриса угла В, ∠AOB =∠COB (дано)⇒
∆ АОВ=∆ СОВ по двум углам при общей стороне ВО ( 2-й признак). ⇒
∠ВОА=∠ВОС.
Т.к. АО и СО - биссектрисы, то и ∠ВАС=∠ВСА. как состоящие из равных половинок. ⇒ ∆ АВС равнобедренный.
Примем ∠ОАС и ∠ОСА равными α. Тогда ∠АОС=180°-2α.
∠АВС=180°-4 α.
Составим уравнение согласно условию:
∠ АОС=3∠ АВС⇒
180°-2α=3(180°-4α). Произведя необходимые вычисления, получим 10α=360°⇒ α=36°
Угол АВС=180°-4•36°=36°.
Углы А и С вдвое больше α, они равны по 72°.
Следовательно, наименьший угол ∆ АВС - угол АВС=36°
∆ АВЕ - равнобедренный ( ∠ВЕА=∠ЕАD как накрестлежащие,
а∠ ВАЕ =∠ЕАD – т.к. АЕ - биссектриса.)
S ∆ ACM=MC•h/2
S ∆ AMD=DM•h/2.
Высота из А у обоих треугольников общая, следовательно, СМ=DM
В ∆ МЕС и ∆ MAD по два равных накрестлежащих угла, равные вертикальные углы и СМ=DM.
Эти треугольники равны по 2-му признаку.⇒ АМ=ЕМ, СЕ=АD и ВЕ=ВС+АD=17.
Т.к. ∆ АВЕ равнобедренный, АВ=ВЕ=17.
В АВЕ М - середина основания АЕ, ВМ - его медиана и высота. ⇒
∆ АВМ - прямоугольный.
По т. Пифагора из ∆ АВМ катет АМ=√(BА²-BM²)=√(17²-8²)=15 ед. длины.