ответ: 5*
решение: мы знаем все углы, это очень хорошо
рассмотрим треугольник образованный после того как мы посторили высоту, он прямоугольный, тк высота это один из катетов жэтого треугольника. Ещё мы знаем угол острого угла данного нам изначально прямоугольного треугольника - это 50*. 180-50-90=40* это один из 3х образовавшихся углов в прямом углу нашего карневого треугольника.
2й угол из тех трех это 45*, так как нам дана биссектриса, которая делит наш прямой угол на два ровных угла по 45*
на и найдем оставшийся 3й угол, весь угол(90*)-45*-40*=5*
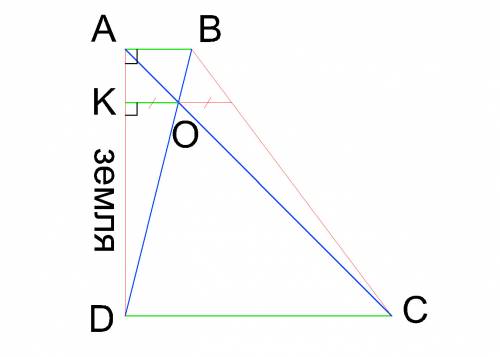
Шесты АВ и ДС как основания образуют прямоугольную трапецию АВСД, а пересечение канатов ВД и СА есть не что иное, как пересечение диагоналей прямоугольной трапеции.
Как известно, отрезок, параллельный основаниям и проходящий через пересечение диагоналей прямоугольной трапеции делится точкой пересечения пополам, и если АВ=х, ДС=у, то длина его равна 2·х·у/(х + у).
Исходя из этого: ОК=2·х·у/(х + у)÷2=х·у/(х + у)
1) ОК=(х·у)÷(х + у)
Как видно, длина ОК никаким образом не зависит от расстояний между шестами, а лишь от их высоты.
2) Если AB=х=2 м, а DC=у=8 м, то ОК=(2·8)÷(2+8)=1,6 м
ответ: длина шеста ОК=1,6 м
Симпатичное условие. :))
То, что в 4угольник можно вписать окружность, сразу определяет порядок сторон.
1,2,4,3 (обход по часовой стрелке).
Суммы противоположных сторон должны быть равны.
На самом деле, возможны еще перестановки, но они отличаются от этой поворотом или зеркальным отражением, то есть эквивалентны этой. Можете их все перебрать, нарисовать - и увидите :).
На этом техническая простота заканчивается - раз этот 4угольник можно вписать в окружность, то сумма противоположных углов равна 180 градусов - поскольку они опираются на дуги, дополняющие друг друга до полной окружности.
Интуитивно понятно, углы между большими сторонами будут меньше - это утверждение ничего не меняет в решении, так что его можно не читать :)
Пусть диагонали d1и d2;
Введем обозначения для косинусов углов (обратите внимание, что именно я обозначаю!) между сторонами.
Пусть косинус угла между сторонами 2 и 4 равен x - тогда косинус угла между сторонами 1 и 3 равен -х; (потому что сумма этих углов 180 градусов)
d1^2 = 4^2 + 2^2 - 2*2*4*x = 1^2 + 3^2 + 2*1*3*x;
отсюда x = 5/11; d1^2 = 140/11;
Аналогично, пусть косинус угла между сторонами 3 и 4 равен y; тогда косинус угла между сторонами 1 и 2 равен -y;
d2^2 = 4^2 + 3^2 - 2*3*4*y = 1^2 + 2^2 + 2*1*2*y;
отсюда y = 5/7; d2^2 = 55/7;
Ясно, что d2 - меньшая диагональ, она равна √(55/7)
Я не уверен, что вы знаете, что cos(x) = - cos(180 - x), но теорему косинусов для случая тупых углов должны были проходить. Так что с чередованием знака все должно быть понятно.