Меньшее основание трапеции равно 4 см,
большее основание равно 36 см,
площадь трапеции равна 240 см²
Объяснение:
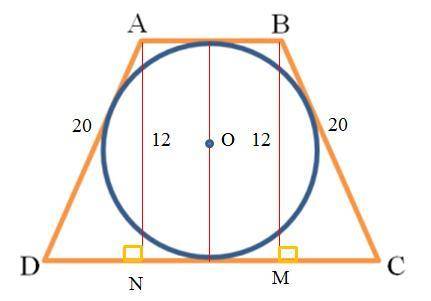
Как известно, в выпуклый четырехугольник ABCD, в нашем случае в трапецию (см. рисунок), можно вписать окружность тогда и только тогда, когда AB+CD=BC+AD, то есть
AB+CD=20+20=40 см
и, следовательно CD=40–AB.
Опустим из вершины A высоту AN, а из вершины B высоту BM. Площадь трапеции определяем через основания и высоту по формуле:
S=(AB+CD)•AN:2=40•12:2=40•6=240 см².
Теперь рассмотрим ΔADN с ∠AND=90°. По теореме Пифагора получаем:
DN²=AD²–AN²=20²–12²=(20–12)•(20+12)=8•32=8²•2²=16²,
то есть DN=16 см.
Так как треугольники ADN и BMC равны (4-ый признак: если катет и гипотенуза одного треугольника соответственно равны катету и гипотенузе другого треугольника, такие прямоугольные треугольники равны), то MC=DN=16 см. С другой стороны
CD=AB+DN+MC=AB+16+16=AB+32.
Приравниваем выражения для CD:
AB+32=40–AB
и находим AB=4 см.
Тогда CD=40–AB=40–4=36 см.
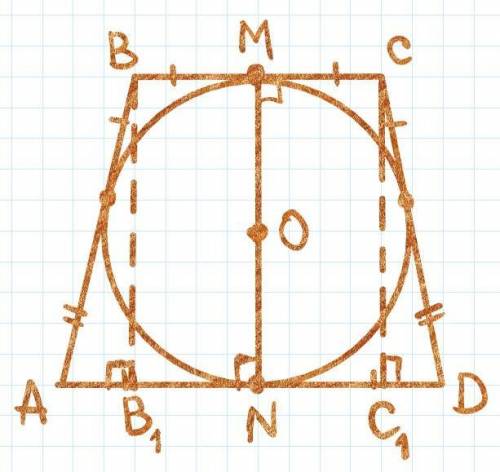
Замечаем, что диаметр вписанной окружности равен высоте трапеции! (см. чертеж!)
Сумма боковых сторон равна сумме оснований (условие того, что в четырехугольник можно вписать окружность):
AD + BC = 40 см (*)
Опустим из вершины B высоту BB₁ (а из вершины C высоту CC₁) и рассмотрим ΔABB₁ (∠B₁ = 90°). По теореме Пифагора получаем:
AB₁² = 20² - 12² = 8 · 32 = 16² ⇒ AB₁ = 16 см
Но 2 · AB₁ = AD - BC = 32 см (**)
Складывая (*) и (**) получаем:
2 · AD = 72 см ⇒ AD = 36 см, BC = 40 - 36 = 4 см
S = (AD + BC) · BB₁ ÷ 2 = 40 · 6 = 240 см²
Даны координаты вершин треугольника: A(−12;−1); B(0;−10); C(4;12).
1) Находим длину стороны АВ.
АВ (с) = √((Хв-Ха)²+(Ув-Уа)²) = √((0-(-12))²+(-10-(-1))²) = √(144 + 81) =
= √225 = 15.
2) Уравнения сторон AB и ВC и их угловые коэффициенты;
Находим векторы АВ и АС:
АВ: (12; -9), ВС:(4; 22).
Получаем уравнения:
АВ: (х + 12)/12 = (у + 1)/(-9),
ВС: х/4 = (у + 10)/22.
Угловые коэффициенты сторон
Кав = Ув-Уа = -9/12 = -3/4 = -0,75.
Хв-Ха
Квс = Ус-Ув = 22/4 = 11/2 = 5,5.
Хс-Хв
3) Угол В между прямыми AB и BC в радианах (градусах) с точностью до двух знаков после запятой. Находим по теореме косинусов.
Находим длины сторон.
АВ (с) = √((Хв-Ха)²+(Ув-Уа)²) = √225 = 15.
BC (а)= √((Хc-Хв)²+(Ус-Ув)²) = √500 = 10√5 ≈ 22,36068.
Векторы ВА: (-12; 9), ВС:(4; 22).
cos В = (-12*4 + 9*22)/(15*10√5 = 150/(150√5) = √5/5.
В = arc cos(√5/5) ≈ 1,107148718 ≈ 1,11 радиан .
4) Уравнение высоты CD и ее длину.
Находим площадь треугольника по формуле:
S=(1/2)*|(Хв-Ха)*(Ус-Уа)-(Хс-Ха)*(Ув-Уа)|.
Подставив координаты точек, получаем S = 150 кв.ед.
Длина СD = 2S/AB = 2*150/15 = 20.
k(CD) = -1/k(AB) = -1/(-3/4) = 4/3.
Уравнение: у = (4/3)х + в. Подставим координаты точки С.
12 = (4/3)*4 + в, отсюда в = 12 - (16/3) = 20/3.
Уравнение CD: y = (4/3)x + (20/3) .
5) Уравнение медианы AE и координаты точки K пересечения этой медианы с высотой CD .
Точка Е как середина ВС: ((0+4)/2=2; (-10+12)/2=1) = (2; 1).
Вектор АЕ: (14; 2)
Уравнение АЕ: (х + 12)/14 = (у + 1)/2.
Приведём к виду с угловым коэффициентом:
у = (1/7)х + (5/7).
Точка К как пересечение AE и CD.
Приравниваем: (1/7)х + (5/7) = (4/3)x + (20/3),
(-25/21)х = (125/21).
Отсюда х(К) = -5, у(К() = 0.
6) Уравнение прямой L, которая проходит через точку K параллельно стороне AB.
Угловой коэффициент Кав -3/4 сохраняется для прямой L.
Уравнение у = (-3/4)х + в.
Для определения значения в подставим координаты точки К.
0 = (-3/4)*(-5) + в, отсюда в = 0 - 15/4 = (-15/4).
Уравнение у = (-4/3)х - (15/4).
7) Координаты точки F(xF , yF ) , которая находится симметрично точке A относительно прямой CD (это перпендикуляр к АВ).
Находим координаты точки Д как точки пересечения высоты СД и стороны АВ. х(Д) = -8, у(Д) = -4.
Тогда x(F) = 2x(D) - x(A) = -16 -(-12) = -4.
y(F) = 2y(D) - y(A) = -8 -(-1) = -7.