3 см
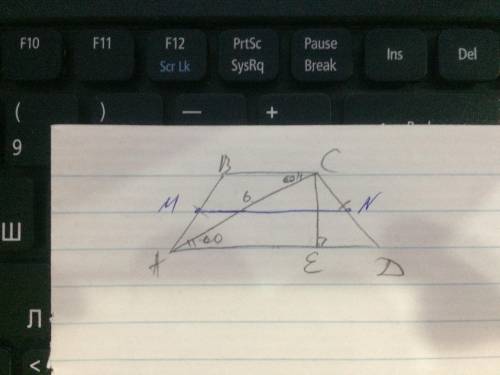
Чертеж в приложении.
Объяснение:
1. Опустим перпендикуляр СЕ в трапеции от меньшего основания к большему. Эта высота разделит большее основание на два отрезка. По свойству равнобедренной трапеции (ЕD - меньший равен половине разности оснований, AE - больший равен полусумме оснований) больший отрезок = средней линии, тк средняя линия тоже = полусумме оснований ;
2. рассм треуг АСЕ- прямоуг (тк СЕ перпенд АD):
тк сумма углов треуг =180, то уг АСЕ= 180-уг САЕ-уг АЕС=180-60-90=30 градусов;
тк АЕ- катет против 30 гр, то АЕ=1/2гипотенузы=1/2 *АС=1/2 * 6=3см
значит, средняя линия MN =3 см
Если что-то непонятно , пишите в комментах.
В основании пирамиды лежит равносторонний тр-к. его высоты, медианы и биссектрисы равны и точкой пересечения делятся в отношении 1/2. т. к бОльшая часть будет являться радиусом описанной окружности а меньшая часть - радиус вписанной окружности.
обозначим основание тр-к АВС. точка пересечения высот О. вершина пирамиды - Н, высота АА1.
ОН по условию =АА1 =9
ОА1= 1/3 АА1= 9/3=3
рассмотрим тр-к НОА1
НА1(апофема) = корень из (9*9+3*3)= корень из 90