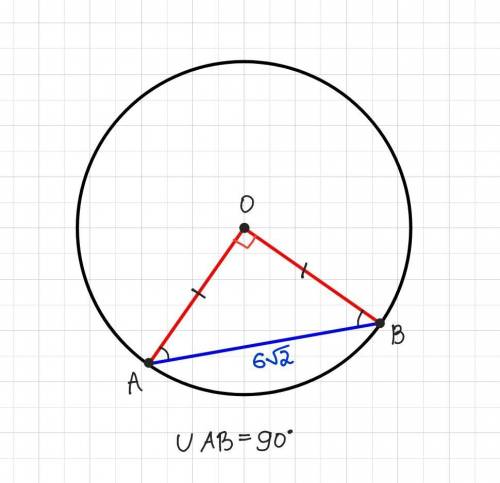
Дано: коло (О; R), AB - хорда, АВ= 6√2 см, ◡АВ= 90°
Знайти: С (довжину кола)
Розв'язання.
Проведемо радіуси ОА і ОВ до кінців хорди АВ. OA=OB=R.
∠АОВ — центральний, це означає що його градусна міра дорівнює градусній мірі дуги, на яку він спирається.
∠АОВ= ◡АВ= 90°.
Як бачимо, ΔАОВ - прямокутний рівнобедрений (оск. ∠АОВ= 90°, ОА=ОВ=R).
Хорда АВ дорівнює 6√2 см, тоді за т.Піфагора у ΔАОВ:
АВ²= ОА²+ОВ²;
(6√2)²= 2ОА²;
72= 2ОА²;
ОА²= 36;
ОА= 6 (–6 не може бути).
Отже, R= 6см.
Тепер знаходимо довжину кола.
За формулою С= 2πR.
С= 2•π•6;
С= 12π, або С= 12•3,14= 37,68 (см)
Відповідь: 12π см або 37,68 см.
В треугольнике ΔАВС два острых угла равны:
∠А = 37°
∠В = 53°
Объяснение:
Всё решение делается на аксиоме: в любом треугольнике все углы в сумме составляют 180°.
1) Высота CD опущена на основание АВ под прямым углом и образует дава прямоугольных треугольника ΔDBС и ΔDCA.
Поскольку в треугольнике ΔDBС угол ∠BDС=90° (как прямой), а ∠BDС=37° (из условия), то
∠DBС = 180° - ∠BDС - ∠BDС = 180° - 90° - 37° = 53°
∠DBС - это ∠В, один из острых углов ΔАВС.
2) Таким же образом находим угол ∠А треугольника ΔАВС.
∠BСА = 90° (прямой), ∠В = 53°,
∠А = 180° - ∠BСА - ∠B = 180° - 90° - 53° = 37°
∠А - второй искомый острый угол.