Построим отрезок BC длины a. Центр O описанной окружности треугольника ABC является точкой пересечения двух окружностей радиуса R с центрами в точках B и C. Выберем одну из этих точек пересечения и построим описанную окружность S треугольника ABC. Точка A является точкой пересечения окружности S к прямой, параллельной прямой BC и отстоящей от нее на расстояние ha (таких прямых две).
8.2.
Построим точки A1 и B1 на сторонах BC и AC соответственно так, что BA1 : A1C = 1 : 3 и AB1 : B1C = 1 : 2. Пусть точка X лежит внутри треугольника ABC. Ясно, что SABX : SBCX = 1 : 2 тогда и только тогда, когда точка X лежит на отрезке BB1, и SABX : SACX = 1 : 3 тогда и только тогда, когда точка X лежит на отрезке AA1. Поэтому искомая точка M является точкой пересечения отрезков AA1 и BB1.
8.3.
Пусть O — центр данной окружности, AB — хорда, проходящая через точку P, M — середина AB. Тогда |AP – BP| = 2PM. Так как РPMO = 90°, точка M лежит на окружности S с диаметром OP. Построим хорду PM окружности S так, что PM = a/2 (таких хорд две). Искомая хорда задается прямой PM.
8.4.
Пусть R — радиус данной окружности, O — ее центр. Центр искомой окружности лежит на окружности S радиуса |R ± r| с центром O. С другой стороны, ее центр лежит на прямой l, параллельной данной прямой и удаленной от нее на расстояние r (таких прямых две). Любая точка пересечения окружности S и прямой l может служить центром искомой окружности.
8.5.
Пусть R — радиус окружности S, O — ее центр. Если окружность S высекает на прямой, проходящей через точку A, хорду PQ и M — середина PQ, то OM2 = OQ2 – MQ2 = R2 – d2/4. Поэтому искомая прямая касается окружности радиуса
Ц
R2 – d2/4
с центром O.
8.6.
Возьмем на прямых AB и CD точки E и F так, чтобы прямые BF и CE имели заданные направления. Рассмотрим всевозможные параллелограммы PQRS с заданными направлениями сторон, вершины P и R которых лежат на лучах BA и CD, а вершина Q — на стороне BC (рис. 8.1). Докажем, что геометрическим местом вершин S является отрезок EF. В самом деле,
SR
EC
= PQ
EC
= BQ
BC
= FR
FC
, т. е. точка S
Рассмотрим вариант, когда прямая имеет угловой коэффициент k>0, тогда она наклонена к положительному направлению оси ОХ под острым углом. Из чертежа видно, что угол наклона не может быть тупым, т.к. тогда S треугольника будет больше 3 .
От координатного угла отсекается ΔВОК , площадь которого S=3. Это прямоугольный треугольник, его площадь равна половине произведения катетов., то есть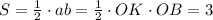
.
Пусть ОК=3 ед. , а ОВ=2 ед. , тогда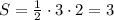
.
Точка В в этом случае будет иметь координаты В(2,0), а точка К(0,-3) .
Подставим в уравнение прямой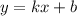
координаты точки А(4,3) и , например, В(2,0), получим:
Или можно использовать то, что точка пересечения с осью ОУ имеет координаты К(0,-3). Тогда уравнение прямой имеет вид: y=kx-3 . И в это уравнение уже подставить координаты точки А(4,3) :
Также можно было составить уравнение прямой, проходящей через две точки А и В ( или А и К) .
Смотри рисунок.