Стороны данного треугольника равны 15 см, 20 см, 30 см. Найдите стороны треугольника с периметром 26 см, подобного данному треугольнику. Покажите, что отношение площадей треугольников ABC и A1B1C1 равно (3)
Объяснение:
Т.к. стороны ΔАВС равны 15 см, 20 см, 30 см , то отношение этих сторон 3:4:6. Такое же отношение сторон будет и в подобном ΔА₁В₁С₁.
Пусть одна часть сторон ΔА₁В₁С₁ будет х , тогда длина сторон будет равна 3х, 4х,6х.
Т.к. Р(А₁В₁С₁) =26 см , то 3х+ 4х +6х =26 , х=2.
Тогда стороны ΔА₁В₁С₁ такие 6 см ,8 см ,12 см.
Найдем коэффициент подобия к=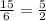 
.
По т. об отношении площадей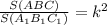 
,получаем
.
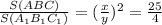А 3 не получается.
Дано: ∠А = ∠А₁; АВ : А₁В₁ = АС : А₁С₁ .
Доказать: ΔАВС подобен ΔА₁В₁С₁.
Доказательство:
Достроим на стороне АС треугольник АВ₂С, в котором углы, прилежащие к стороне АС, равны углам в треугольнике А₁В₁С₁ (как на рисунке) .
Тогда ΔАВ₂С подобен ΔА₁В₁С₁ по двум углам. Запишем отношение сторон в этих треугольниках:
АВ₂ : А₁В₁ = АС : А₁С₁.
Сравним полученную пропорцию с данной в условии:
АВ : А₁В₁ = АС : А₁С₁
Значит, АВ₂ = АВ.
Но тогда ΔАВС = ΔАВ₂С по двум сторона и углу между ними (АС - общая, АВ₂ = АВ и ∠А = ∠А₁ = ∠1 по условию).
Итак, ΔАВС = ΔАВ₂С, а ΔАВ₂С подобен ΔА₁В₁С₁, значит
ΔАВС подобен ΔА₁В₁С₁.
Доказано.