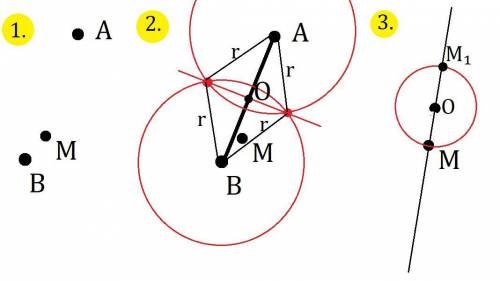
Пусть O - середина AB, нам нужно построить точку симметричную точке M относительно точки O, это я к тому, что точки A и B даны только для того чтобы определить точку O, сам отрезок при вычислении симметрии нам не понадобится.
(см. рис. 2) Соединим A и B. Из точки A проведём окружность радиусом r, при это r должно быть зрительно больше половины отрезка (можно взять хоть всю длину). Из точки B проведём окружность радиусом r. Эти две окружности пересекутся в двух точках, соединяем из, прямая соединяющая эти две точки пересечёт наш отрезок посередине. Отмечаем эту середину O и стираем всё остальное, кроме точки M. (см. рис. 3)Теперь через точки M и O проводим прямую, из точки O проводим окружность радиусом OM, она пересечёт прямую в точке M и M₁; M₁ - и будет той точкой, которую нам надо построить.
Если точки O и M совпадают, то задача не имеет смысла.
Площадь основания - площадь ромба - равна
So=(1/2)*d*D =(1/2)3*4=6 ед².
Диагонали ромба взаимно перпендикулярны и делятся точкой пересечения пополам. Тогда
сторона ромба равна по Пифагору:
а=4*√[(D/2)²+(d/2)²]=4*√(4+2,25)=2,5.
Sб=Р*Н (Р - периметр, Н - высота призмы - боковое ребро).
Sб=10*5=50 ед².
S=2*So+Sб=12+50=62 ед².