Объяснение:
найти площу плоскої фігури, що утворена лініями:
y2-2y-3x+1=0, 3x-3y-7=0.
Розв'язання: Проаналізуємо рівняння кривих, якими обмежена фігура.
y2-2y-3x+1=0, (y-1)2=3x - парабола з вершиною у точці (1;0) і гілками вправо.
3x-3y-7=0, y=x-7/3 - пряма.
Із системи рівнянь знайдемо точки перетину параболи з прямою:
При розв'язуванні квадратного рівняння знаходимо "ікси", а далі з другого рівняння системи обчислюємо "ігрики".
Графік фігури, площу якої шукаємо, наведено на рисунку
подвійний інтеграл
Розставимо межі в області D:
-1≤y≤6, ;
Знайдемо площу фігури через подвійний інтеграл:
знаходження площі
ответ: КО=√119
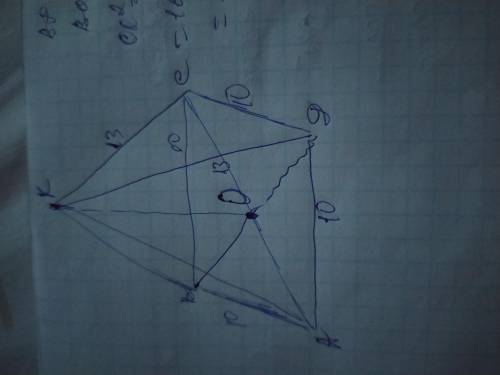
Объяснение: обозначим вершины основания пирамиды А В С Д а её высоту КО. В основании правильной четырёхугольной пирамиды лежит квадрат, поэтому все стороны у основания равны. Проведём диагональ ВД. Она делит квадрат на 2 равных равнобедренных прямоугольных треугольника, в которых стороны основания являются катетами а диагонали гипотенузой. В равнобедренном прямоугольном треугольнике гипотенуза больше катета в √2 раз, поэтому ВД =АС=10√2. Диагонали квадрата пересекаясь делятся пополам поэтому АО=СО=ВО=ДО=10√2/2=5√2см.
Рассмотрим полученный ∆СОД. Он прямоугольный где КОи ДО- катеты а КД- гипотенуза. Найдём высоту КО по теореме Пифагора: КО²=КД²-ДО²=
=13²-(5√2)²=169-25×2=169-50=119;
КО=√119см
AB=44 см
Примем AK за x
Тогда KB = x-12
При этом AK+KB=AB=44
x+x-12=44
2x=56
x=28
AK=28
KB=16