
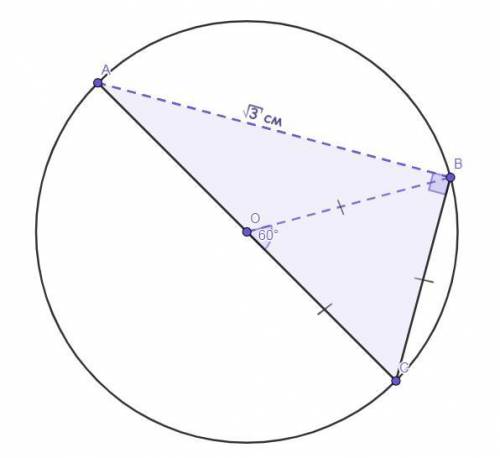
На круге размещены токчи А, В и С так, что АС - диаметр круга, а хорду ВС видно с центра окружности круга под углом в 60°. Найдите радиус круга, если АВ = 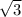 см.
см.
- - -
Дано :Круг.
Точка О - центр данного круга.
Точка А ∈кругу.
Точка В ∈кругу.
Точка С ∈кругу.
АС - диаметр круга.
∠ВОС = 60°.
АВ = 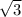 см.
см.
ОС = ? (или ОА, это неважно, так как они равны).
Решение :∠АВС - вписанный (по определению), так ещё и опирается на диаметр АС, следовательно, ∠АВС = 90° (так как диаметр "стягивает" дугу в 180°).
Рассмотрим ΔАВС - прямоугольный.
ОС = ОА (так как радиусы одной окружности). Тогда отрезок ОВ - медиана (по определению), причём проведённая к гипотенузе (АС - гипотенуза, так как лежит против угла в 90°).
В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна её половине.Следовательно -
ОВ = ВС = ОС.
Тогда ΔОВС - равносторонний (по определению).
Каждый угол равностороннего треугольника равен 60°.Следовательно -
∠ВОС = ∠ОВС = ∠С = 60°.
Тогда -
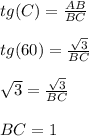
BC = 1 см.
ответ :1 см.
да, да, нет
Объяснение:
Правило:
Длина любой стороны треугольника меньше суммы длин двух других сторон.
Проверим, выполняется ли это условие для наших отрезков.
а) 9; 9; 9;
9 < 9 + 9
9 < 18 - условие выполняется, значит, может. Это будет равносторонний треугольник.
б) 9, 12,13
9 < 12 +13 → 9 < 25
12 < 9 + 13 → 12 < 22
13 < 9 + 12 → 13 < 21
Все три условия выполняются. Эти отрезки могут быть сторонами треугольника.
в) 12, 13, 49
12 < 13 + 49 → 12 < 62
13 < 12 + 49 → 13 < 61
49 < 12 + 13 → 49 < 25 - это неравенство неверно, 49 > 5.
Следовательно, треугольника со сторонами 12,13,49 существовать не может.
вот, ответ смотри на фото