Привести общее уравнение прямой к нормальному виду в каждом из следующих случаев: 1) 4х —3у—10 = 0; 2) x —y+10 = 0; 3) 12х — 5у + 13 = 0; 4) х + 2 = 0; 5) 2х — у -√5= 0.
а) Для решения этой задачи нам понадобится знание о биссектрисе прямого угла в прямоугольном треугольнике. Биссектриса является отрезком, который делит прямой угол на два равных угла. Известно, что в прямоугольном треугольнике прямой угол равен 90 градусов, поэтому биссектриса будет делить этот угол на два равных угла по 45 градусов каждый.
Для нахождения длины биссектрисы воспользуемся теоремой Пифагора. Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
В данной задаче известны длины катетов: один равен 6 см, а другой - 12 см. Обозначим их как a = 6 см и b = 12 см. Нам нужно найти длину биссектрисы.
Обозначим длину биссектрисы как c. По теореме Пифагора, у нас будет следующее уравнение:
c^2 = a^2 + b^2
Подставляем значения:
c^2 = 6^2 + 12^2
c^2 = 36 + 144
c^2 = 180
Чтобы найти длину биссектрисы c, возьмем квадратный корень из обеих частей уравнения:
c = √180
Давайте упростим это:
c = √(9 * 20)
c = 3√20
Таким образом, длина биссектрисы прямого угла равна 3√20 см.
б) Для решения этой задачи, нужно знать, что биссектриса делит противолежащий угол на два равных угла. Также можно использовать теорему биссектрисы, которая говорит, что отношение длин сегментов, на которые биссектриса делит противолежащую сторону, равно отношению длин других сторон треугольника.
В данной задаче, известно, что сторона AC равна 7 см, сторона CB равна 9 см, и AD = CD. Давайте обозначим длину биссектрисы как x.
С помощью теоремы биссектрисы, получаем следующее уравнение:
AC/AD = BC/BD
Подставим известные значения в уравнение:
7/x = 9/x
Теперь решим это уравнение:
7x = 9x
7 = 9
Мы получаем противоречивое уравнение, которое не имеет решения. Здесь возникает проблема, поскольку данное уравнение не имеет решения, значит биссектрисы данного треугольника нет.
Таким образом, мы не можем найти длину биссектрисы треугольника ∆АВС в данной задаче.
Для доказательства, что AABC W ADBE, мы должны показать, что все углы и стороны треугольника AABC соответствуют углам и сторонам треугольника ADBE.
1. Углы:
У нас есть два вертикальных угла: угол EBC и угол DAB. Вертикальные углы равны, поэтому угол EBC = угол DAB. Также углы внутри треугольника AABC равны: угол BAC = угол BCA = угол ABC, так как это равносторонний треугольник.
2. Стороны:
Мы знаем, что AD IBC и CE TAB. IBC - это опора, поэтому сторона AB равна стороне BC, и сторона AD равна стороне IB. Следовательно, AB = BC и AD = IB.
Теперь, чтобы доказать, что AABC W ADBE, мы можем использовать свойство равных треугольников, которое говорит, что если мы имеем два треугольника с равными соотношениями сторон и углов, то они равны в целом.
У нас есть следующие совпадения:
- AB = BC (из AD IBC)
- AD = IB (из AD IBC)
- угол EBC = угол DAB (вертикальные углы)
Исходя из этих схем, мы можем заключить, что треугольники AABC и ADBE равны в соответствии с теоремой равных треугольников.
1. x=(3y+10)/4
2. x=y-10
3. x=(5y-13)/12
4. x=-2
5. x=(y+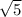 )/2
)/2