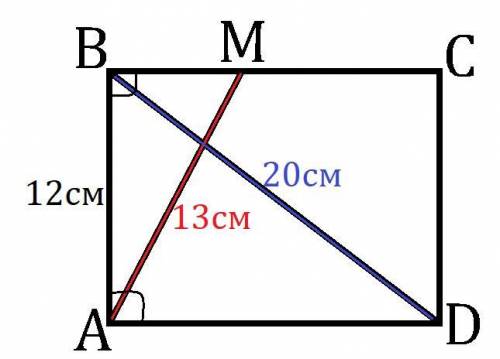
В прямоугольном ΔBAD (∠A=90°):
AB=4·3см, BD=4·5см значит, по Египетскому треугольнику AD=4·4см=16см.
AD = BC = 16см, как противоположные стороны прямоугольника ABCD.
В прямоугольном ΔABM (∠B=90°):
AB=12см, AM=13см значит, по Пифагоровой тройке BM=5см;
Ну или по теореме Пифагора BM = √(AM²-AB²) = √(13²-12²) = √((13-12)(13+12)) = √25 = 5 см.
MC = BC-BM = 16-5 = 11 см
S(AMCD) = S(ABCD) - S(ABM) = AB·AD - 
AB·BM = 12·16-12·5:2 = 6·(32-5) = 6·27 = 162 см²
ответ: MC=11см и S(AMCD)=162см².
Можно было найти S(AMCD), как площадь трапеции, основания которой MC=11см, AD=16см и высота CD=AB=12см. Тогда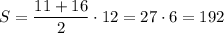 
см².
Для прямоугольного треугольника справедлива теорема Пифагора : квадрат гипотенузы равен сумме квадратов катетов.
Треугольник с заданными сторонами является прямоугольным.
25² = 7² + 24²
625 = 49 + 576 = 625
Пусть коэффициент пропорциональности равен k, тогда пропорциональные стороны треугольника будут 7k, 24k, 25k
(25k)² = (7k)² + (24k)²
625k² = 49k² + 576k² ⇒ 625k² = 625k²
Для треугольника со сторонами 7k, 24k, 25k тоже справедлива теорема Пифагора, значит, треугольник является прямоугольным.