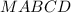- правильная четырехугольная пирамида, около которой описан конус 
⊥ 
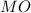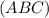
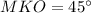
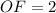см
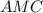- осевое сечение конуса, где 
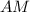и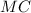 
- образующие конуса
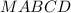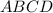
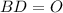
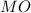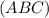
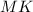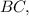- правильная четырехугольная пирамида, 
∩ 
⊥ 
⊥ 
тогда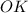 
⊥ 
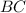и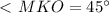 
как линейный угол двугранного угла 
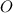- центр окружности, описанной около квадрата 
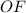, т. е. ⊥ 
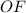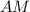
тогда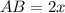 
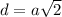, где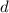 
- диагональ квадрата, 
- сторона квадрата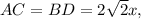
( как диагонали квадрата)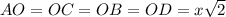
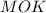- прямоугольный, равнобедренный, следовательно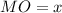 
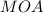- прямоугольный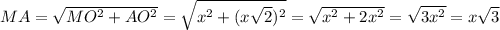
,
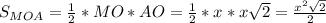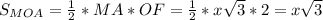
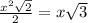
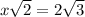
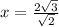
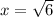
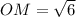см
см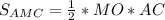
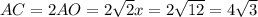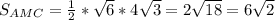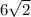(см ²)
см²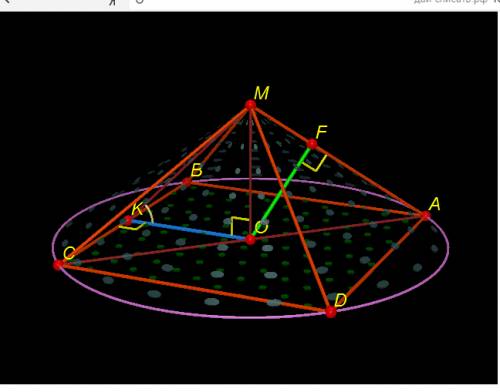
а). Точка, симметричная данной относительно оси 0Х, лежит на прямой, проходящей через эту точку перпендикулярно оси 0Х, на расстоянии, равном расстоянию от данной точки до оси 0Х. То есть это точка В(-1,5;-2).
б). Точка, симметричная данной относительно оси 0Y, лежит на прямой, проходящей через эту точку перпендикулярно оси 0Y, перпендикулярно оси 0Y, на расстоянии, равном расстоянию от данной точки до оси 0Y. То есть это точка С(1,5;2).
в). Точка, симметричная данной относительно начала координат, лежит на прямой, проходящей через данную точку и начало координат, на расстоянии, равном расстоянию от данной точки до начала координат.
То есть это точка D(1,5;-2).
соболезную брат, но это силшком трудно
Объяснение: