1)
A(6,0)
B(0,8)
(3,4)
10
2)
O(3,7)
(x-3)^2+(y-7)^2=65
y=2x-5
Объяснение:
1) Если прямая пересекается с осью ox, то координата y точки пересечения равна 0. Подставляем это значение в уравнение прямой и, решая его, находим координату x точки пресечения.
(вычисления на скрине 1)
A(6,0)
B(0,8)
Координаты середины отрезка вычисляются по формуле (скрин 2)
Длина отрезка вычисляется по формуле (скрин 3)
2) Если прямые пересекаются, то координаты точки пересечения удовлетворяю каждому уравнению. Приравняем и решим относительно x, а потом подставим значение в любое уравнение (скрин 4)
Найдем радиус окружности (расстояние от O до B) и запишем уравнение окружности (скрин 5.1)
Параллельность = равенство угловых коэффициентов. Исходя из этого найдем b и запишем уравнение (скрин 5.2)
ꟷꟷꟷꟷꟷꟷ
Не забывайте сказать " "! и, если ответ удовлетворил, то выберите его как "Лучший"
Бодрого настроения и добра!
Успехов в учебе!
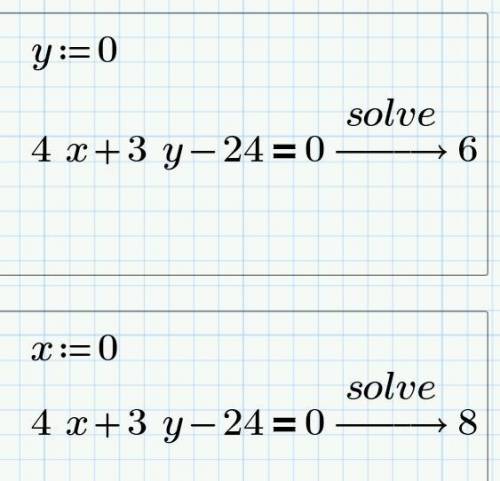
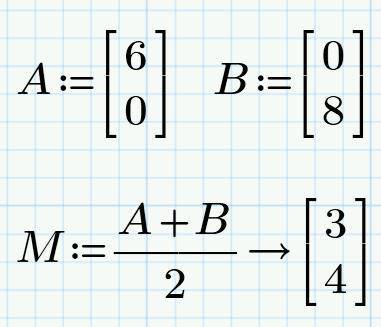
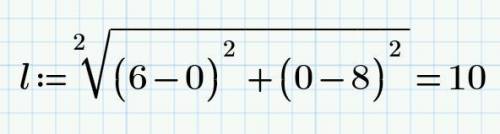
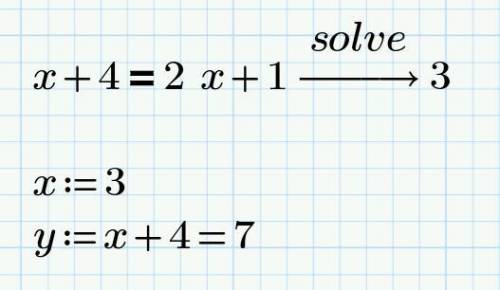
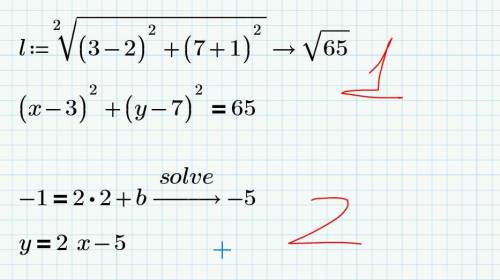
Половина диагонали m√2/2, высота и боковое ребро образуют прям-ный тр-ник с катетом m√2/2 и углом против него α/2.
tg (α/2) = (m√2/2) / H
а) Высота равна H = (m√2/2) / tg (α/2) = m√2*ctg (α/2) / 2
б) Боковое ребро b = (m√2/2) / sin (α/2)
в) Апофема (высота боковой грани) L^2 = b^2 - m^2 = (m^2/2) / sin^2 (α/2) - m^2
L = m*√ [1 - 2sin^2 (α/2)] / sin (α/2) = m*√(cos α) / sin (α/2)
Угол между боковой гранью и плоскостью основания
sin β = H / L = m√2*ctg(α/2) / 2 * sin(α/2) / (m*√(cos α)) = √2*cos(α/2) / (2√(cos α))
г) Двугранный угол при боковом ребре - это не знаю.