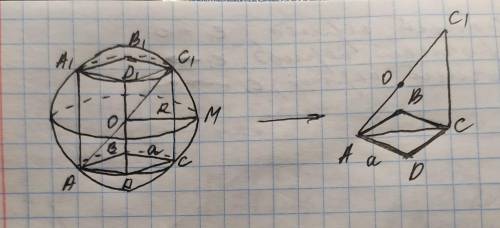
Так как призма вписана в шар, то своими углами она касается шара, и, следовательно, радиус шара будет равен также отрезку, проведенному из центра шара до одного из углов призмы (рисунок прилагается)
Рассмотрим треугольник АСС1, где С1О=ОА как радиусы описанного шара, то есть АС1=2R.
Треугольник прямоугольный, так как призма прямоугольная с высотой СС1. Основание АС равнo АВ√2 (как диагональ квадрата АВСD) = a√2, => по теореме Пифагора можем найти высоту СС1:
√(АС1²-АС²)=√((2R)²-(a√2)²)=√(4R²-2a²), и, как следствие, площадь боковой поверхности:
Sбок=Росн•h=4a•CC1=4a√(4R²-a²)
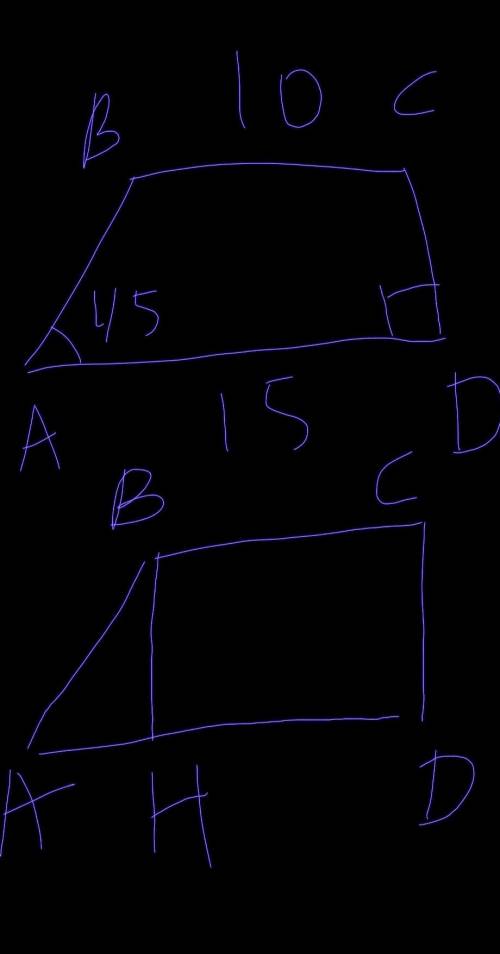
Проведём высоту из точки В к основанию АD и рассмотрим треугольник АВН: угол при высоте равен 90°, угол при основании 45° (из условия), => мы имеем прямоугольный равнобедренный треугольник, => оставшаяся часть прямой AD – отрезок AH равен AD-HD=15-10=5 см. (HD=BC=10, так как высота BH отсекает от стороны AD отрезок, равный BC из-за проведения высоты), => если треугольник АВН – прямоугольный равнобедренный, то AH=HB=5, а четырёхугольник BCDH в свою очередь является прямоугольником, => меньшая боковая сторона трапеции CD=BH=5 см
Шаровым сегментом называется часть шара, отсеченная от него плоскостью. Если OP – радиус шара, перпендикулярый отсекающей плоскости, то точку P назовем в этом случае полюсом шара. Высотой шарового сегмента называется отрезок PO1, соединяющий полюс шара с центром основания шарового
Шаровой сегмент можно рассматривать как тело, образованное вращением кругового сегмента вокруг диаметра, перпендикулярного его хорде. Формулу объема шарового сегмента выводят так же, как и формулу объема шара, но интегрируют на промежутке (0; H) (H – высота шарового сегмента):
Следовательно, объем шарового сегмента равен 1/2пи*H^2*(3R-H) где подставляй радиус и высоту сегмента.успеха.