Радиус окружности с центром в точке о равен 10. если длина дуги ав равна 4пи,то радианная мера угла аов равна?

👇

Увидеть ответ

Ответ:

елизавета4щ

24.03.2020

Длина дуги (L) равно произведению соответствующего ей угла (альфа:) (в радинах) на радиус (R)

4Пи=альфа*10

альфа=4Пи/10=2Пи/5

4,6(45 оценок)

Открыть все ответы

Ответ:

ПолинаПашкова14

24.03.2020

1. От точки А строим угол, равный данному (описано в первом

варианте) и на полученной второй его стороне откладываем отрезок

АВ, равный данной гипотенузе. Из точки В опускаем перпендикуляр на

прямую "а". Для этого:

Из точки В проводим окружность любого радиуса R, чтобы пересекла

прямую "а" в точках G и Q. Из точек G и Q тем же радиусом проводим

две дуги, пересекающиеся в точке M. Прямая ВМ - искомый перпендикуляр.

На пересечении прямых ВМ и "а" ставим точку С.

Соединяем точки А,В и С и получаем прямоугольный треугольник АВС

с прямым углом <C и с заданными гипотенузой и острым углом.

2. На прямой "а" откладываем отрезок, равный одной из сторон, например, АС. Проводим окружности с центрами в точках А и С радиусами, равными двум другим сторонам, например, АВ и СВ соответственно. В точке пересечения этих окружностей получаем точку В. Треугольник построен.

3. На прямой "а" откладываем отрезок, равный стороне АВ, к которой проведена высота СН. Проводим окружность радиуса ВС с центром в точке В. Из точки В к прямой "а" восстанавливаем перпендикуляр и на нем откладываем отрезок ВР, равный высоте СН. Из точки Р проводим перпендикуляр к отрезку ВР и в точке пересечения этого перпендикуляра с проведенной ранее окружностью ставим точку С.

Соединив точки А,С и В получаем искомый треугольник.

P.S. Построение перпендикуляра к прямой в заданную точку не описываю - это стандартное построение.

4,4(14 оценок)

Ответ:

Катя881118

24.03.2020

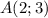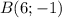Ці точки лежать на серединному перпендикулярі точок A(2;3) та B(6;-1) . Знайдемо координати точки — середини відрізка :

$M\left(\dfrac{2+6}{2};\dfrac{3+(-1)}{2}\right)=M(4;1)$

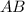Щоб знайти кутовий коефицієнт серединного перпендикуляра, знайдемо кутовий коефіцієнт прямої :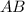

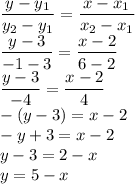
$\dfrac{y-y_1}{y_2-y_1}=\dfrac{x-x_1}{x_2-x_1}\\\dfrac{y-3}{-1-3}=\dfrac{x-2}{6-2}\\\dfrac{y-3}{-4}=\dfrac{x-2}{4}\\-(y-3)=x-2\\-y+3=x-2\\y-3=2-x\\y=5-x$

Коефіцієнт перпендикулярної прямої дорівнює $-\dfrac{1}{-1}=1$ . Застосуємо формулу прямої за кутовим коефицієнтом і точкою, через яку пряма проходить: