A1. Две прямые на плоскости называются параллельными, если они:
4) не пересекаются
А2. Один из признаков параллельности двух прямых гласит:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
А3. Выберите утверждение, являющееся аксиомой параллельных прямых:
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной
А4. Если две параллельные прямые пересечены секущей, то:
Соответственные углы равны
А5. Если прямая перпендикулярна одной из двух параллельных прямых, то:
Она перпендикулярна и другой
А6. Всякая теорема состоит из нескольких частей:
Условия и заключения
А7. При пересечении двух прямых секущей образуются углы, имеющие специальные названия:
Накрест лежащие, соответственные, односторонние
А8. Аксиома – это:
Положение геометрии, не требующее доказательства
А9. Выберите утверждение, которое является признаком параллельности прямых:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
А10. Если прямая не пересекает одну из двух параллельных прямых, то:
Другую прямую она тоже не пересекает
или
С другой прямой она совпадает
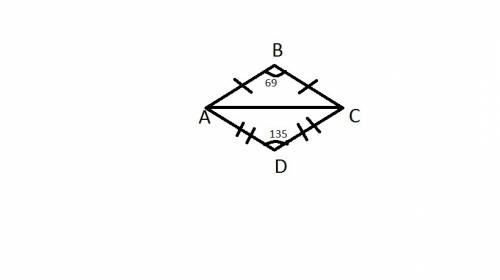
решение:дополнительное построение: проведем диоганаль АС
1) рассмотрим треугольник АВС , т.к. АВ=ВС следовательно треугольник равнобедренный а значит по свойству равнобедренного треугольника угол ВАС = ВСА а т.к. в треугольнике сумма углов = 180 градусов следовательно найдем угол А и С.
(180-69)/2=55,5 градуса
2) аналогично вычисляем угол ДАС и ДСА, получаем (180-135)/2=22,5 градуса
3) из этих вычислений мы сможем получить угол А сложив угол ВАС и ДАС 55,5+22,5=78градусов
ответ: угол А=78 градусам
ВАК=37°
АКВ=113°
Объяснение:
ВАК=74/2=37° (биссектриса делит угол пополам)
АКВ=180°-37°-76°=113°