Єтот тест
Контрольный тест по теме: "Прямоугольные треугольники. Построение треугольника по трем элементам"
Система оценки: 5 балльная
Список во теста
Во Найдите углы треугольников, на которые медиана разбивает равносторониий треугольник.
Варианты ответов
определить невозможно
60°,40°,80°
60°,45°,45°
60°,30°,90°
Во Найдите сумму внешних углов треугольника, взятых по одному при каждой вершине.
Варианты ответов
определить невозможно
270°
360°
180°
Во Концы хорды окружности соединены с центром. Найдите углы получившегося треугольника, если один из них на 36 градусов больше другого. Рассмотрите все случаи.
Варианты ответов
48°,48°,84° или 38°,71°,71°
48°,48°,84° или 36°,72°,72°
78°,60°,42° или 48°,48°,84°
38°,71°,71° или 36°,72°,72°
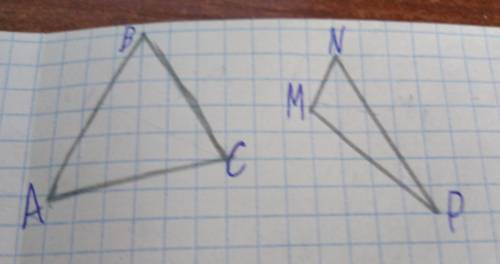
Во Варианты ответов
KM < MN
KN = MN
MK = MN
MK > KN
KN + KM > MN
Во Одна из сторон равнобедренного треугольника на 12 см меньше другой. Найдите стороны треугольника, если его периметр равен 33 см. Рассмотрите все случаи.
Варианты ответов
13 см, 13 см, 7 см или 7 см, 7 см, 19 см.
3 см, 15 см, 15 см
3 см, 15 см, 15 см или 7 см, 7 см, 19 см
7 см, 7 см, 19 см
Во Варианты ответов
⊿ ABC - разносторонний
∠ KLM=90° ⇒KL ∥ BC
∠ BCO внешний угол ⊿ ABC
∠ DKN внешний угол ⊿ KLM
⊿ ABC - равнобедренный
⊿ ABC - тупоугольный
⊿ ABC - прямоугольный
Во Варианты ответов
BC и MO
нет параллельных отрезков
BA и OK
Во Во Определите вид треугольника по углам и стоорнам, если его углы относятся как:
Варианты ответов
разносторонний
равнобедренный
равнобедренный
остроугольный
прямоугольный
тупоугольный
равносторонний
Получите комплекты видеоуроков
Биология 7 класс. Позвоночные животные
Обществознание 7 класс ФГОС
Введение в общую биологию и экологию 9...
Химия 9 класс ФГОС
Мир мультимедиатехнологий 6 класс
Электронная тетрадь по информатике 5...
Алгебра 8 класс ФГОС
Электронная тетрадь по ОБЖ 5 класс
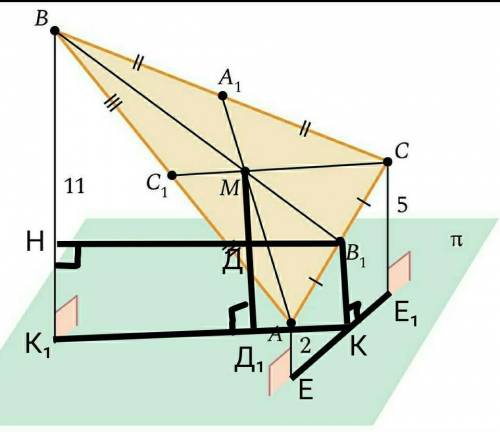
МД₁=6
Объяснение:
Искомым расстоянием от точки пересечения медиан М, до плоскости π является отрезок МД₁.
Обозначим высоты от стороны АС к плоскости π: В₁К, АЕ, СЕ₁. Соединим точки Е и Е₁. Получим трапецию ЕАСЕ₁. В₁К || АЕ || СЕ, так как они перпендикулярны плоскости π. По теореме Фалеса если параллельные прямые, пересекая стороны угла отсекают равные отрезки на одной его стороне, то они отсекают равные отрезки и на второй стороне угла, поэтому если АВ₁=В₁С, то ЕК=КЕ₁. → В₁К – средняя линия трапеции ЕАСЕ₁.
В₁К=(ЕА+Е₁С)÷2=(2+5)÷2=7÷2=3,5
Проведём перпендикуляры В₁Н и КК₁ к стороне ВК₁, получили трапецию В₁КК₁В.
В₁Н делит ВК₁, что К₁Н=В₁К=3,5, тогда ВН=11–3,5=7,5.
Рассмотрим ∆ВВ₁Н, он прямоугольный, ВН и В₁Н – катеты, ВВ₁ – гипотенуза. Медианы треугольника, пересекаясь, точкой пересечения делятся на отрезки в отношении 2 : 1, начиная от вершины треугольника, поэтому ВМ : МВ₁=2 : 1 и по теореме Фалеса ДН : В₁Д=2 : 1. МД || ВН, и МД отсекает от ∆ВВ₁Н подобный ему ∆МВ₁Д. Стороны ∆ВВ₁Н имеют 3 части (2+1=3), а стороны ∆МВ₁Д – одну часть. Пусть МД=х, запишем пропорцию:
МД : ВН=1 : 3
Произведение крайних членов пропорции равно произведению средних:
МД•3=ВН•1
3х=7,5•1
3х=7,5
х=7,5÷3
х=2,5
ДД₁=В₁К=НК₁=3,5
МД₁=МД+ДД₁=2,5+3,5=6
Объяснение:
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону