Найдите объём правильной четырёхугольной пирамиды, боковое ребро которой равно 12 см и образует с высотой угол в 30°.
==========================================================
▪В основании правильной четырёхугольной пирамиды лежит квадрат. Вершина такой пирамиды проецируется в точку пересечения диагоналей квадрата. Диагонали квадрата равны, взаимно перпендикулярны и точкой пересечения делятся пополам.▪Рассмотрим ΔАОМ: ∠АМО = 30° ⇒ катет, лежащий против угла в 30°, равен половине гипотенузы ⇒ АО = АМ/2 = 12/2 = 6 см ⇒ AO = BO = CO = DO = 6 смПо т. Пифагора:АМ² = АО² + ОМ²ОМ² = АМ² - АО² = 12² - 6² = 144 - 36 = 108ОМ = 6√3 см▪Рассмотрим ΔАОВ: по т. ПифагораАВ² = АО² + ВО² = 6² + 6² = 36 + 36 = 72АВ = 6√2 смV mabcd = S осн. • H / 3 = AB² • MO / 3 = ( 6√2 )² • 6√3 / 3 = 72 • 6√3 / 3 = 144√3 см³ОТВЕТ: 144√3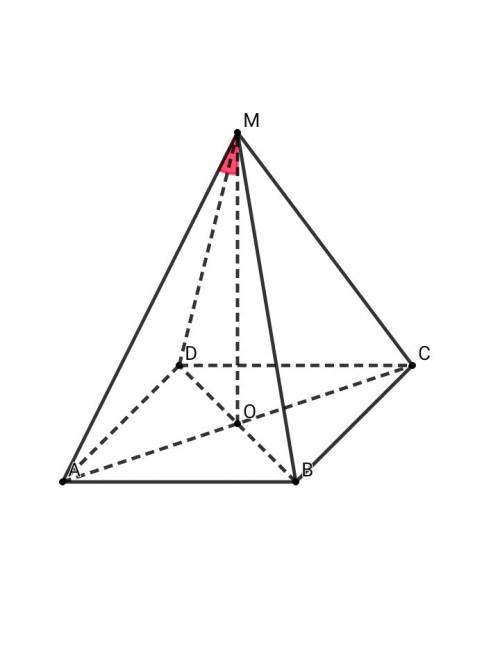
Забавная задачка, мне понравилась)
Правда, сначала недопонял, но потом сообразил, что Вы опечатались: основаниуе ВC=5, ведь DС - одно из бедер!)
Давайте тогда, чтоб путаницу из-за опечатки убрать, все проговорим:
Трапеция АВСД, основания АД=2 и ВС=5, высота трапеции - она же малая диагональ - ВД. Рисуйте и - поехали!
Идея решения у меня такая: раз малая диагональ перпендикулярна основаниям, то она делит трапецию на два прямоугольных треугольника.
У каждого из них, конечно же, как полагается, сумма углов равна 180 градусам.
Ну, а сумма углов, которые непрямые, равна 90 градусов. У каждого, а у обоих-двоих вместе аж 180!
то есть можно вот что написать:
САД+АВД+ВСД+СДВ равна 90+90=180 градусов.
Условие говорит, что, что сумма углов А и С равна 90.
Из этого всего естественно, как говорится, вытекает, что сумма углов АВД и ВДС тоже равна 90 градусов!
И это - основа моего решения.)
Ибо из этого я делаю вывод о подобии треугольников АВД и ДВС! (Нужно пояснять, или удалось ясно высказаться?)
Это подобие мы используем для того, чтоб вычислить длину той самой коротокой диаганали:
Она бОльший катет треугольника АВД и мЕньший катет треугольника ДВС.
АД относится к ДВ так же, как ДВ относится к ВС.
АД и ВС известны, можно считать:
2/ДВ=ДВ/5
ДВ в квадрате=10
ДВ= квадратный корень из 10
Ну, а теперь совсем просто:
Опускаем вертикаль из С на продолжение АД. Назовем точку пересечения К.
Длинная диагональ - это гипотенуза бааальшого треугольника АСК с катетами
АК = АД + ВС = 2+5 = 7 и
СК = ВД = как посчитали, квадратному корню из 10.
Проще нету: длина АС равна корню квадратному из суммы квадратов этих катетов,. т.е. из суммы 49 и 10
АС= корню квадратному из 59.
Это 7,681 и т.д...
Число, конечно, довольно противное, но по-моему все правильно...
Ура?
Ура!))