Смотри вложение.............................
ответ: 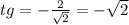
Кстати, если надо, то этот угол =125.3[/tex]
В основании пирамиды SABCD лежит параллелограмм ABCD с центром O. Точка M лежит на отрезке SO, причём OM:MS =1:3.
а) Постройте сечение пирамиды плоскостью, проходящей через
прямую AM параллельно прямой BD.
б) В каком отношении плоскость сечения делит ребро SC?
Объяснение:
а)Проведем через М прямую В₁D₁║ВD .
«Если заданная прямая a, не лежащая в плоскости α, параллельна прямой b, которая принадлежит плоскости α, тогда прямая a параллельна плоскости α.»
Получим точки В₁ и D₁. В плоскости ( АСS) продолжим прямую АМ до пересечения с SC. Соединим В₁-Р и D₁-Р .Полученное сечение искомое.
б)В равнобедренном ΔАСS( т.к пирамида правильная) , высота SO-является медианой. По т. Менелая
СР/РS*(SM/OM)*(AO/AC)=1,
СР/РS*(3/1)*(AO/2AO)=1,
СР/РS*(3/1)*(1/2)=1,
СР/РS=2/3

пусть середина стороны АВ т. К
пересечением пл. (альфа) и пл. треугольника (АВС) является прямая k
прямая k параллельна стороне ВС
в противном случае, она должна пересечь прямую(ВС)
НО точка пересечения должна принадлежать также пл. (альфа)
а это НЕВОЗМОЖНО -
пл. (альфа) и ВС не имеют точек пересечения - по условию они параллельны
значит прямая k ПАРАЛЛЕЛЬНА ВС
прямая k является секущей сторон АВ и АС и делит их на пропорциональные отрезки
отсюда следует , что прямая k и плоскость альфа проходит также через середину стороны АС.
отрезок прямой k (между сторонами АВ и АС)- это средняя линия треугольника АВС
если начертить квадрат, то мы увидим, что угол между этими плоскостями, это угол в прямоугольном треугольнике между гипотенузой и коротким катетом, где короткий катет - 1/2 диагонали FH, а длиннй катет - ребро FF1 = 3
находим FH по теореме пифагора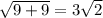
1/2 FH = 3/2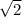
тангенс, это отношение противолежащего катета к прилежащему и = FF1 / 1/2 FH =
3 / 3/2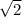 =
= 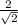
ответ: тангенс угла между плоскостями EHG и EGF1 =