Дано точки A(1 ; √3; 3) B( 1; 0; 2) C(-1; -1; 3) D(-1; 0; 3)
Найти угол между векторами AB и CD
Объяснение:
Координаты вектора АВ(1-1 ;0-√3 ;2-3) или АВ(0;-√3-1) ;
Координаты вектора CD(0 ;1;0).
Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними: АВ*CD= |АВ|* |CD|*cos∠(АВ;CD) ,
АВ*CD=0*0+(-√3)*1+(-1)*0=-√3 , ( скалярное произведение в координатах);
|АВ|=√( 0²+(-√3)²+(-1)²)=√(0+3+1)=2 ;
|CD|=√( 0²+1²+0²)=1,
Подставим в АВ*CD= |АВ|* |CD|*cos∠(АВ;CD) ,
-√3=2*1*cos∠(АВ;CD) , cos∠(АВ;CD) =√3/2⇒ ∠(АВ;CD)=150°
Объяснение:
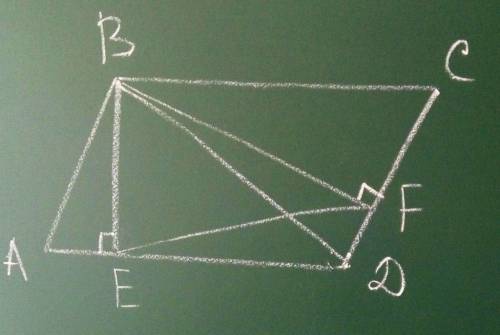
ABCD-параллелограмм⇒∠C=∠A, AD║BC
∠C=∠A⇒sin∠C=sin∠A
AD║BC⇒∠CBD=∠ADB
BE⊥AD⇒∠BED=90°
BF⊥AD⇒∠BFD=90°
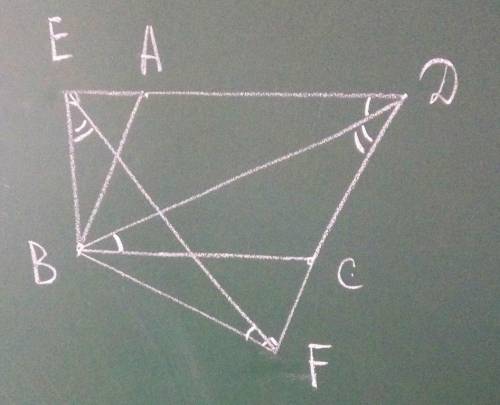
∠BED=∠BFD=90°⇒ точки B,E,F,D лежат на одной окружности с диаметром BD. Тогда по теореме о равенстве вписанных углов имеем ∠BEF=∠BDF, ∠BDE=∠BFE
∠BFE=∠BDE=∠CBD
∠BEF=∠BDC, ∠BFE=∠CBD⇒ΔBEF~ΔBDC ч.т.д.
Из ΔBEF по теореме синусов имеем EF/sinEBF=2R, где R-радиус описанной окружности около ΔBEF⇒ R=0,5BD, так как это та самая окружность которая содержит точки B,E,F,D.
EF/sinEBF=2R⇒EF=2RsinEBF=BDsinC=BDsinA=15·0,4=6
Случаи того что угол В острый или тупой разбираются аналогично.
Есть такое правило, что биссектрисы трапеции прилегающие к одной стороне, пересекаются под прямым углом и точка пересечения лежит на средней линии.
Это доказывается из равенства углов, которые образуются при пересечении паралельных линий третьей, а т.к она и биссектриса, то тоже углы равны . Нарисуй чертёж и всё будет понятно.
1. СD = V ( 24ˇ2 + 18ˇ2) = V900 = 30
2.FG = 16 - ( 13/2 + 15/2) = 2