АВС-прямоугольный треугольник, высота- ВН=4,8
АВ=3х, ВС=4х
Рассмотрим треуг. АВН:
ВН и АН-катеты, АВ-гипотенуза:
По т.Пифагора: АН^2= АВ^2 - BH^2
9х^2=23,04
x^2=2,56
x=1,6
Рассмотрим треуг. ВНС:
по.т. Пифагора:
HC^2=BC^2-BH^2
16x^2=23,04
x^2=1,44
x=1,2
ответ: АН=1,6 ; НС=1,2
Відповідь:V=15см³
Пояснення:
Объем такого параллелепипеда равен произведению его трех измерений.
Одно из этих измерений равно 5см. Пусть оставшиеся измерения равны X и Y. Тогда периметр параллелепипеда равен 4*X+4*Y+4*5 =36см. Или
X+Y=4 см. (1) Х=4-Y (2).
Площадь полной поверхности параллелепипеда:
S=2*(5*X)+2*(5*Y)+2*X*Y=46 см². Или
5*X+5*Y+X*Y=23 см². Или
5(X+Y)+X*Y=23 см². Подставим значение (1):
5*4+X*Y=23 => X*Y=3. Подставим значение из (2):
Y²-4Y+3=0. Решаем это квадратное уравнение:
Y1=1 см. => X1=3см
Y2=3см. => X2 =1см.
Тогда объем параллелепипеда равен 1*3*5=15см³.
ответ: V=15см³.
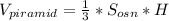
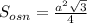
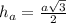
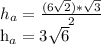

Треугольник АВС, высота АД на гипотенузу ВС. Треугольники АВС и АДВ подобны острому углу В, треугольники АВС и АДС подобны по острому углу С. Значит треугольники АВД и АДС подобны.
АВ/АС=АД/ВД, 3/4=4,8/ВД, ВД= 6,4
АС/АВ=ДС/АД, 3/4=4,8/ДС ДС=6,4