118°, 118°, 62°, 62°
Объяснение:
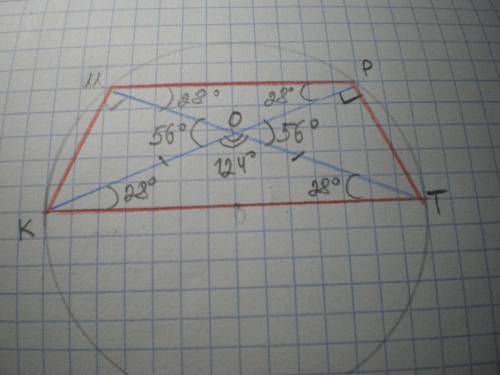
Дано: КМРТ - трапеция, МК=РТ, КТ=D (окружности), КР и МТ - диагонали, ∠РОТ=∠МОК=56°. Найти ∠К, ∠М, ∠Р, ∠Т.
Решение: ΔКМТ=ΔТРК, т.к. КР=МТ как диагонали равнобедренной трапеции, КМ = РТ по условию, сторона КТ - общая. Значит, ∠ОКТ=∠КТО.
∠КОТ=180-56=124°; ∠ОКТ=∠КТО=(180-124):2=28°.
ΔМОР; ∠МРО=∠ОМР=∠ОКТ=∠КТО=28° как внутренние накрест лежащие при МР║КТ и секущих МТ и КР.
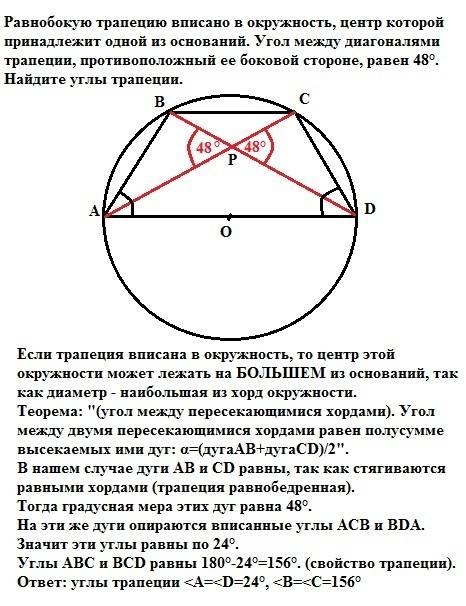
∠КМТ=∠КРТ=90° как углы, опирающиеся на диаметр окружности.
∠М=∠Р=90+28=118°
∠К=∠Т=180-118=62° по свойству углов трапеции, прилежащих к боковой стороне
Решить, значит найти все стороны и углы этого треугольника
1) Найдем угол А: А=180-60-105=15 градусов ( по теореме о сумме углов треугольника)
2) По теореме синусов найдем АС: 7/sin15 гр=АС/ sin60 гр ( теорема: стороны треугольника пропорциональны синусам противолежащих углов)
7/0.2588=АС/0.8660 (sin 15гр и 60 гр нашли по таблице Брадиса)
АС=6.062/02588 =23.4 см
3) АВ можно найти двумя либо через теорему косинусов либо через теорему синусов. Найдем по теореме косинусов АВ2= ВС2+АС2-2АВВСcos угла С (Теорема косинусов квадрат стороны треугольника равен сумме квадратов других его сторон минус удвоенное произведение этих сторон на косинус угла меду ними. В общем виде: а2=в2+с2-2вс соsa) АВ2=49+529-322cos105 (сos105=-cos75 -по формулам приведения)
Подставьте значения и посчитайте