а)уравнение стороны AB = -8х+4у+84=0, BC=2х+14у-6=0, AC=-10х-10у-30=0. Можно представить эти уравнения с угловым коэффициентом в виде y = kx + a. Для этого перенесем все значения кроме y в правую часть, например: 4y = 8x - 84. Затем разделим правую часть на коэффициент 4. Получим: y = 2x - 21. б)уравнение высоты CH можно составить, зная координату точки Н(8;-5) СН = 6х+12у+12=0. в)уравнение медианы AM можно составить, зная координату точки М(3;0) АМ = -9х-3у+27=0. г)точку N пересечения медианы AM и высоты CH: так как заданный треугольник равнобедренный (а=в=14,1421), то высота на сторону АВ является и медианой. Поэтому точка N - центр тяжести треугольника. N(4;-3). д)уравнение прямой,проходящей через вершину C параллельно стороне AB = у-2х-9=0 или у = 2х+9. е)расстояние от точки C до прямой AB - это высота СН = 13,4164.
Если на одной из двух прямых отложить несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
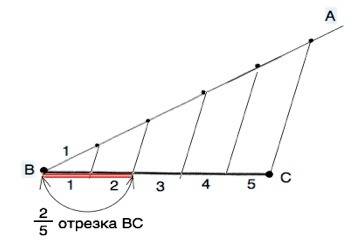
Пусть дан отрезок ВС.
От конца В отрезка начертить луч и на нем от В отметить через равные промежутки 5 точек. Из пятой точки провести прямую через т.С отрезка ВС и провести параллельно ей прямые, пересекающие отрезок ВС. Этими прямыми ВС будет разделен на 5 равных частей. Любые две соседние части равны 2/5 исходного отрезка ВС.
В
Д
С А
из тр-ка АВС угол А=90-35=55град
в тр-ке угол СДА=90град (СД-высота), а угол ДСА= 90- угол А=90-55=35град