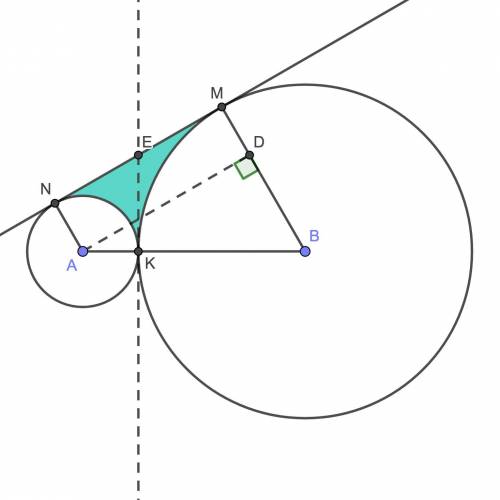
1) Отразим рисунок относительно прямой AB, окружности перейдут сами в себя, а K – перейдёт в точку K', симметричную относительно прямой AB. Если K не лежит на AB, то K и K' не совпадают, и K' – тоже точка касания, чего быть не может.
2) Радиусы, проведённые в точку касания, перпендикулярны касательной, поэтому AN и BM перпендикулярны NM, а тогда параллельны, ANMB – прямоугольная трапеция.
Проведём высоту трапеции AD. ANMD – прямоугольник, поэтому MD = AN = r, тогда BD = 2r. Кроме того, AB = AK + KB = 4r, поэтому ∠DAB = 30° (противолежащий катет равен половине гипотенузы), а по теореме Пифагора  .
.
Площадь трапеции ANMB равна 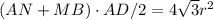
Площадь сектора KAN с центральным углом 90° + 30° = 120° = π/3 равна 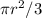
Площадь сектора KBM с центральным углом 90° - 30° = 60° = π/6 равна 
Площадь искомой фигуры
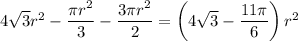
Tреугольник ABC прямоугольный, так как
АВ² - ВС² = 169 - 25 = 144 = 12²
То есть соотношение сторон подчиняется теореме Пифагора.
Следовательно, АС = 12 и наименьшим углом является угол А
sin A = BC/AB = 5/13; cos A = AC/AB = 12/13;
tg A = sin A/cosA = 5/13 : 12/13 = 5/12
ctg A = 1/tg A = 12/5 = 2.4
Объяснение:
это только первый второй ну этого