Рассмотрим параллелограмм АВСД (см. рисунок) стороны которого: АВ=32 см, ВС=40 см. Из угла АВС проведем перпендикуляр ВЕ и расстояние между вершинам тупых углов ВД Рассмотрим треугольник АВЕ: Угол АЕВ=90 градусов, Гипотенуза АВ=32 см, Катет АЕ=16 см (по условию задачи) По теореме Пифагора найдем второй катет (высоту): ВЕ= √(АВ^2-АЕ^2)= √(32^2-16^2)= √(1024-256)= √768 см. Теперь рассмотрим треугольник BДE: ДЕ=АД-АЕ=40-16=24 см. ВЕ=√768 см. Угол ВЕД=90 градусов По теореме Пифагора найдем ВД: ВД=√(ВЕ^2+ВД^2)= √((√768)^2+24^2))= √(768+576)= √1344=8√21 см или приблизительно 36,66 см. ответ: расстояние между вершинами тупых углов равно 8√21 см
Вариант 1.
Так как <ABC = 45°, то: <A = 90-45 = 45°.
И так как острые углы друг другу равны, то прямоугольный треугольник — равнобёдренный, тоесть: BC = AC.
//Росстояние от точки A — до плоскости "α" — это и есть катет AC.//
У нас есть 2 условия: AB+BC = 17; AC-BC = 7.
И так как эти 2 катета равны — то составим систему только с одной переменной "x":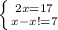
Э-э, стоп, что? Разность двух равных чисел не равна 7-и? Недопустимо!
Задача с ошибкой, если один и острых углов равен 45°, то второй тоже. Катеты равны, тоесть их разность не может быть равной 7-и.
Вариант 2.
Проигнорируем определение острого угла 45-градусов, представим, что нам известно только это: AC+BC = 17; AC-BC = 7.
Этой информации нам достаточно, чтобы найти катеты.
Но только на этот раз — переменных будет 2: AC = "x"; BC = "y".
Вывод: AC = 12.