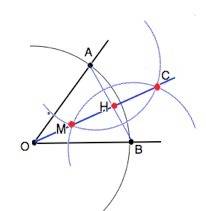
Ставим ножку циркуля в вершину О угла и проводим полуокружность, пересекающую стороны угла в т.А и В.
ОА=ОВ=R. Соединим точки А и В. Треугольник АОВ равнобедренный.
Из т. А и В как из центра раствором циркуля R больше половины расстояния АВ проводим полуокружности.
Точки их пересечения и вершина угла лежат на одной прямой. Соединяем их.
Для окружностей МС - общая хорда, АВ соединяет их радиусы. АВ и МС взаимно перпендикулярны (свойство).⇒ ОН - высота равнобедренного треугольника, следовательно, по свойству высоты равнобедренного треугольника она же – его биссектриса. Биссектриса ОС построена.
Соединение средин сторон треугольника называется средней линией треугольника. Она расположена параллельно третьей стороне, а длина ее равна половине длины этой стороны. Поэтому можно утверждать, что и стороны меньшего треугольника так же будут относится как 4:3:5.
Так как периметр треугольника, образованного средними линиями равен 3,6 дм, а стороны относятся как 4:3:5, то выразим это следующим образом (Для удобства вычисления переведем все величины в сантиметры 1 дм = 10 см):
4х – длина отрезка АВ;
3х – длина отрезка ВС;
5х – длина отрезка АС;
4х + 3х + 5х = 36;
12х = 36;
х = 36 / 12 = 3;
АВ = 4 · 3 = 12 см;
ВС = 3 · 3 = 9 см;
АС = 5 · 3 = 15 см.
ответ: стороны треугольника, образованного средними линиями равны 12 см = 1,2 дм, 9 см = 0,9 дм, 15 см = 1,5 дм.